题目内容
(1)如图1的图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D;
(2)阅读下面的内容,并解决后面的问题:
如图2,AP、CP分别平分∠BAD、∠BCD,
若∠ABC=36°,∠ADC=16°,求∠P的度数;
【解析】
∵AP、CP分别平分∠BAD、∠BCD ∴∠1=∠2,∠3=∠4,
由(1)的结论得: ,
,
①+②,得2∠P+∠2+∠3=∠1+∠4+∠B+∠D.
∴∠P= (∠B+∠D)=26°.
(∠B+∠D)=26°.
① 如图3, 直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,求∠P的度数;
② 在图4中,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论,无需说明理由.
③ 在图5中,AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论,无需说明理由.(本题8分)

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目



 是
是 与
与 的交点,当
的交点,当 时,求PB与PC的比值;
时,求PB与PC的比值; ,且满足且
,且满足且 ,请借助图3补全图形,并求
,请借助图3补全图形,并求 的长.
的长.
 配方后变形为( )
配方后变形为( ) B.
B.
 D.
D.
 ,并把它的解集在数轴上表示出来.(本题5分)
,并把它的解集在数轴上表示出来.(本题5分) ,并写出不等式组的整数解.(本题5分)
,并写出不等式组的整数解.(本题5分) ,当
,当 时,则
时,则 的取值范围是 .
的取值范围是 .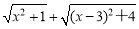 的几何意义,并求它的最小值.
的几何意义,并求它的最小值.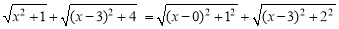 ,如图,建立平面直角坐标系,点P(x,0)是x轴上一点,则
,如图,建立平面直角坐标系,点P(x,0)是x轴上一点,则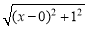 可以看成点P与点A(0,1)的距离,
可以看成点P与点A(0,1)的距离, 可以看成点P与点B(3,2)的距离,所以原代数式的值可以看成线段PA与PB长度之和,它的最小值就是PA+PB的最小值.
可以看成点P与点B(3,2)的距离,所以原代数式的值可以看成线段PA与PB长度之和,它的最小值就是PA+PB的最小值.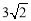 ,即原式的最小值为
,即原式的最小值为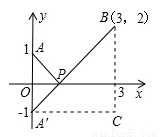
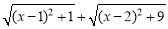 的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B 的距离之和.(填写点B的坐标)
的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B 的距离之和.(填写点B的坐标)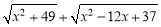 的最小值.
的最小值. 中,A(0,2),B(0,6),动点C在直线
中,A(0,2),B(0,6),动点C在直线 上.若以A、B、C三点为顶点的三角形是等腰三角形,则点C的个数是( )
上.若以A、B、C三点为顶点的三角形是等腰三角形,则点C的个数是( )