题目内容
10．
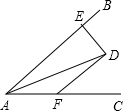如图，∠BAC=30°，AD平分∠BAC，DE⊥AB于E，DF∥AB，已知AF=4cm，则DE的长为（ ）| A． | 1cm | B． | 2cm | C． | 3cm | D． | 4cm |
分析 由角平分线的定义和平行线的性质易得DF=AF=4m，∠DFC=∠BAC=30°，作DG⊥AC于G，根据角平分线的性质可得，DG=DE，在Rt△FDG中，易得DG=$\frac{1}{2}$DF=2cm，即可求得DE．
解答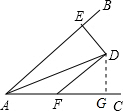 
解：作DG⊥AC于G，
∵AD平分∠BAC，
∴∠BAD=∠CAD，DE=DG，
∵DF∥AB，
∴∠ADF=∠BAD，∠DFC=∠BAC=30°，
∴∠ADF=∠CAD，
∴DF=AF=4m，
∴Rt△FDG中，DG=$\frac{1}{2}$DF=2cm，
∴DE=2cm．
故选B．
点评 此题主要考查角平分线、平行线的性质和直角三角形中30°锐角所对直角边等于斜边的一半，作辅助线是关键．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
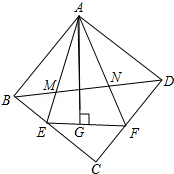如图，在正方形ABCD中，△AEF的顶点E，F分别在BC、CD边上，高AG与正方形的边长相等，且∠EAF=45°，连BD分别交AE、AF于点M、N，若EG=4，GF=6，BM=3$\sqrt{2}$，则MN的长为5$\sqrt{2}$．
19．
如图，AO⊥OB，若∠AOC=50°，则∠BOC的度数是（ ）
如图，AO⊥OB，若∠AOC=50°，则∠BOC的度数是（ ）| A． | 20° | B． | 30° | C． | 40° | D． | 50° |
