题目内容
6.抛物线y=kx2-7x-7的图象和x轴有交点,则k的取值范围是k≥-$\frac{7}{4}$且k≠0.分析 根据二次函数的定义得到k≠0,根据△=b2-4ac决定抛物线与x轴的交点个数得到△=(-7)2-4k•(-7)≥0,然后求出两不等式的公共部分即可.
解答 解:根据题意得k≠0且△=(-7)2-4k•(-7)≥0,
解得k≥-$\frac{7}{4}$且k≠0.
故答案为k≥-$\frac{7}{4}$且k≠0.
点评 本题考查了抛物线与x轴的交点:对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;
△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.注意二次项系数不为0.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
17.若一个多边形的内角和等于1440°,则这个多边形是( )
| A. | 四边形 | B. | 六边形 | C. | 八边形 | D. | 十边形 |
14.如果a2-8a+m是一个完全平方式,则m的值为( )
| A. | -4 | B. | 16 | C. | 4 | D. | -16 |
1.在数轴上,点A表示-3,从点A出发,沿数轴移动5个单位长度到达点B,则点B所表示的数为( )
| A. | 2 | B. | -8 | C. | 2或-8 | D. | 以上均不对 |
16.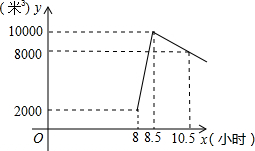 星期天8:00∽8:30,燃气公司给平安加气站的储气罐注入天然气,注完气之后,一位工作人员以每车20米3的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(米3)与时间x(小时)的函数关系如图所示.
星期天8:00∽8:30,燃气公司给平安加气站的储气罐注入天然气,注完气之后,一位工作人员以每车20米3的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(米3)与时间x(小时)的函数关系如图所示.
(1)8:00~8:30,燃气公司向储气罐注入了8000米3的天然气;
(2)当x≥8.5时,求储气罐中的储气量y(米3)与时间x(小时)的函数关系式y=-1000x+18500;
(3)正在排队等候的20辆车加完气后,储气罐内还有天然气9600米3;
(4)这第20辆车在当天9:00之前不能加完气;
其中说法正确的有( )
 星期天8:00∽8:30,燃气公司给平安加气站的储气罐注入天然气,注完气之后,一位工作人员以每车20米3的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(米3)与时间x(小时)的函数关系如图所示.
星期天8:00∽8:30,燃气公司给平安加气站的储气罐注入天然气,注完气之后,一位工作人员以每车20米3的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(米3)与时间x(小时)的函数关系如图所示.(1)8:00~8:30,燃气公司向储气罐注入了8000米3的天然气;
(2)当x≥8.5时,求储气罐中的储气量y(米3)与时间x(小时)的函数关系式y=-1000x+18500;
(3)正在排队等候的20辆车加完气后,储气罐内还有天然气9600米3;
(4)这第20辆车在当天9:00之前不能加完气;
其中说法正确的有( )
| A. | (1)(2) | B. | (2)(3) | C. | (1)(2)(3) | D. | (1)(2)(3)(4) |