��Ŀ����
��ͼ����ƽ��ֱ������ϵ�У���֪������y=ax2+bx+c��x����A��2��0����B��6��0�����㣬��y���ڵ�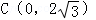 ��
��
��1����������ߵĽ���ʽ��
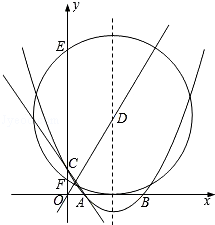
��2�����������ߵĶԳ�����ֱ��y=2x���ڵ�D������D��x�����У���D��y���ڵ�E��F���㣬���ӻ�EF�ij���
��3��PΪ���������ڵڶ�����ͼ���ϵ�һ�㣬PG��ֱ��x�ᣬ����Ϊ��G����ȷ��P���λ�ã�ʹ�á�PGA�������ֱ��AC��Ϊ1��2�����֣�
�������ѧУ���꼶����
�⣺��1����������y=ax2+bx+c������A��2��0����B��6��0���� ��
��
�� ��
��
��� ��
��
�������ߵĽ���ʽΪ�� ����3�֣�
����3�֣�
��2����֪�����ߵĶԳ�����x=4��
��x=4����y=2x����y=8��
���D��������4��8����
�ߡ�D��x�����У����D�İ뾶Ϊ8����1�֣�
����DE��DF����DM��y�ᣬ����Ϊ��M��
��Rt��MFD��FD=8��MD=4��
���MDF=60�㣬
���EDF=120�㣻��2�֣�
���ӻ�EF�ij�Ϊ�� ����1�֣�
����1�֣�
��3����ֱ��AC�Ľ���ʽΪy=kx+b��
��ֱ��AC������ ��
��
�� ��
��
��� ��
��
��ֱ��AC�Ľ���ʽΪ�� ����1�֣�
����1�֣�
��� ��PG��ֱ��AC��N��
��PG��ֱ��AC��N��
���N����Ϊ ��
��
��S��PNA��S��GNA=PN��GN��
�����PN��GN=1��2����PG��GN=3��2��PG= GN��
GN��
�� =
=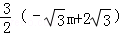 ��
��
��ã�m1=��3��m2=2����ȥ����
��m=��3ʱ�� =
= ��
��
���ʱ��P������Ϊ ����2�֣�
����2�֣�
����PN��GN=2��1����PG��GN=3��1��PG=3GN��
�� =
= ��
��
��ã�m1=��12��m2=2����ȥ����
��m=��12ʱ�� =
= ��
��
���ʱ��P������Ϊ ��
��
��������������P����Ϊ ��
�� ʱ����PGA�������ֱ��AC�ֳ�1��2�����֣���2�֣�
ʱ����PGA�������ֱ��AC�ֳ�1��2�����֣���2�֣�


 ��
�� �Ķ�������Ϊ
�Ķ�������Ϊ 
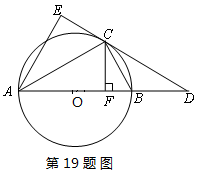 ��1����֤��DE�ǡ�O�����ߣ�
��1����֤��DE�ǡ�O�����ߣ�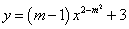 ��һ�κ�������ôm��ֵ�ǡ�������������������������������
��һ�κ�������ôm��ֵ�ǡ�������������������������������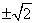 ��
��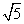 ���Ը�������Ľ����������ABCD�������
���Ը�������Ľ����������ABCD�������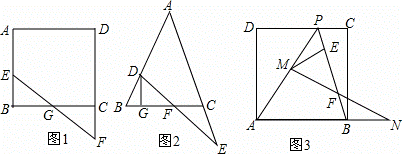
 xny3��ͬ�����m+n��ֵ����������������
xny3��ͬ�����m+n��ֵ����������������