题目内容
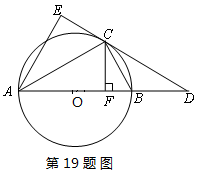
如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线上的一点,AE⊥CD交DC的延长线于E,CF⊥AB于F,且CE=CF.
 (1)求证:DE是⊙O的切线;
(1)求证:DE是⊙O的切线;
(2)若AB=6,BD=3,求AE和BC的长.
(1)连接OC.
∵AE⊥CD,CF⊥AB,CE=CF,
∴∠1=∠2.
∵OA=OC,
∴∠2=∠3.
∴∠1=∠3.
∴OC∥AE.
∴OC⊥CD.
∴DE是⊙O的切线.
(2)∵AB=6,
∴OB=OC= AB=3.
AB=3.
在Rt△OCD中,OC=3,OD=OB+BD=6,
∴∠D=30°,∠COD=60°.
在Rt△ADE中,AD=AB+BD=9,
∴AE= AD=
AD= .
.
在△OBC中,∵∠COD=60°,OB=OC,∴△OBC是等边三角形.
∴BC=OB=3.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的值为0,则
的值为0,则 的值等于
的值等于 ,换个角度有AC1=AB-C1B=1
,换个角度有AC1=AB-C1B=1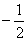 ;AC2=
;AC2=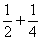 ,换个角度有AC2=AB-C2B=1
,换个角度有AC2=AB-C2B=1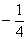 ;…ACn=
;…ACn=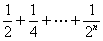 ,换个角度有AC=AB-CnB=____。(用含n的代数式表示)由此我们得到
,换个角度有AC=AB-CnB=____。(用含n的代数式表示)由此我们得到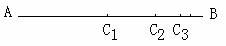
 B.相切 C.相交 D.相交或相切
B.相切 C.相交 D.相交或相切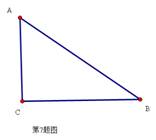
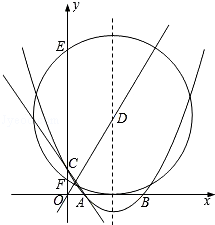
 上运动, 当⊙P与x轴相切时,圆心P的坐标为_____________。
上运动, 当⊙P与x轴相切时,圆心P的坐标为_____________。 
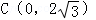 .
.