题目内容
19．三角形两边的长分别是9和7，第三边的长是方程x2-12x+20=0的一个实数根，则此三角形的周长是（ ）| A． | 18 | B． | 26 | C． | 26或18 | D． | 20 |
分析 先利用因式分解法解方程得到x1=10，x2=2，再利用三角形三边的关系可得三角形第三边长为10，然后计算三角形的周长．
解答 解：x2-12x+20=0，
（x-10）（x-2）=0，
x-10=0或x-2=0，
所以x1=10，x2=2，
∵2+7=9，
∴三角形第三边长为10，
∴三角形的周长=9+7+10=26．
故选B．
点评 本题考查了解一元二次方程-因式分解法：先把方程的右边化为0，再把左边通过因式分解化为两个一次因式的积的形式，那么这两个因式的值就都有可能为0，这就能得到两个一元一次方程的解，这样也就把原方程进行了降次，把解一元二次方程转化为解一元一次方程的问题了（数学转化思想）．也考查了三角形三边的关系．
练习册系列答案
相关题目
9．
如图EF∥GF∥IJ∥BC，共有（ ）对相似的三角形．
如图EF∥GF∥IJ∥BC，共有（ ）对相似的三角形．| A． | 4对 | B． | 5对 | C． | 6对 | D． | 7对 |
10．若△ABC的三边a，b，c满足a2+b2-8a-10b+29+|c-3|=0，则（ ）
| A． | △ABC是直角三角形且∠C=90° | B． | △ABC是锐角三角形 | ||
| C． | △ABC是直角三角形且∠B=90° | D． | △ABC是直角三角形且∠A=90° |
7．下列方程是关于x的一元二次方程的是（ ）
| A． | ax2+bx+c=0 | B． | $\frac{1}{{x}^{2}}+\frac{1}{x}$=2 | C． | x2+2x=x2-1 | D． | 3（x+1）2=2（x+1） |
14．据北京市气象局统计，今年的雾霾天气比常年同期多一倍以上，为1954年以来同期最多，表一是国家环保总局所公布的空气质量级别表．现从市环保监测站提供的资料中，随机抽取了今年1至3月份中30天空气综合的污染指数如下：
30，32，40，42，45，45，77，83，85，87，90，113，127，153，167，
38，45，48，53，57，64，66，77，92，98，130，184，201，235，243．
请根据空气质量级别表和抽查的空气综合污染指数，解答以下问题：
（1）先填写频率分布表二中未完成的空格，并求出统计数据中的中位数和众数；
（2）请根据抽样数据，估计该市今年（按360天计算）空气质量是优良的天数．
空气质量级别表一
频率分布表二
30，32，40，42，45，45，77，83，85，87，90，113，127，153，167，
38，45，48，53，57，64，66，77，92，98，130，184，201，235，243．
请根据空气质量级别表和抽查的空气综合污染指数，解答以下问题：
（1）先填写频率分布表二中未完成的空格，并求出统计数据中的中位数和众数；
（2）请根据抽样数据，估计该市今年（按360天计算）空气质量是优良的天数．
空气质量级别表一
| 空气污染指数 | 空气质量 | 级别 |
| 0-50 | 一级 | 优 |
| 51-100 | 二级 | 良 |
| 101-150 | 三级 | 轻度污染 |
| 151-200 | 四级 | 中度污染 |
| 201-300 | 五级 | 重度污染 |
| ＞300 | 六级 | 严重污染 |
| 分组 | 频数 | 频率 |
| 0-50 | 0.30 | |
| 51-100 | 12 | 0.40 |
| 101-150 | ||
| 151-200 | 3 | 0.10 |
| 201-300 | 3 | 0.10 |
| 300 | 0 | 0.00 |
| 合计 | 30 | 1.00 |
4．
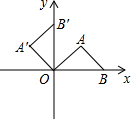将等腰直角三角形AOB按如图所示放置，然后绕点O逆时针旋转90°至△A′OB′的位置，点B的横坐标为2，则点A′的坐标为（ ）
将等腰直角三角形AOB按如图所示放置，然后绕点O逆时针旋转90°至△A′OB′的位置，点B的横坐标为2，则点A′的坐标为（ ）| A． | （1，1） | B． | （-1，1） | C． | （1，-1） | D． | $（-\sqrt{2}，\sqrt{2}）$ |
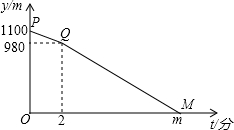A、B相距1100米，甲从A地出发，乙从B地出发，相向而行，甲比乙先出发2分钟，乙出发7分钟后与甲相遇．设甲、乙两人相距y米，甲行进的时间为t分钟，y与t的函数关系式如图，回答下列问题
9．已知xy≠1，且有3x2+2014x+7=0，7y2+2014y+3=0，则$\frac{x}{y}$的值等于（ ）
| A． | $\frac{3}{7}$ | B． | $\frac{7}{3}$ | C． | -$\frac{2014}{7}$ | D． | -$\frac{2014}{3}$ |