Question

15．已知△ABC的三边AB=11cm，AC=7cm，BC=6cm，AD、AD′是内、外角平分线，求DD′的长．

Answer 1

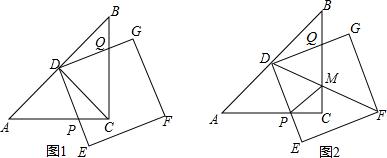
分析 过A作AM⊥BC于M，过C作CE⊥AB于E，过D作DF⊥AB于F，设AE=x，由勾股定理得；AC²-AE²=BC²-BE²，求出AE=$\frac{67}{11}$，BE=$\frac{54}{11}$，于是得到CE=$\sqrt{A{C}^{2}-A{E}^{2}}$=$\frac{12\sqrt{10}}{11}$根据三角形的面积公式得到$\frac{1}{2}$AM•BC=$\frac{1}{2}$AB•CE，求出AM=2$\sqrt{10}$，根据角平分线定理得到$\frac{CD}{BD}=\frac{AC}{AB}=\frac{7}{11}$求出CD=$\frac{7}{3}$，BD=$\frac{11}{3}$由△BDF∽△BCE，得到$\frac{BD}{BC}=\frac{DF}{CE}=\frac{BF}{BE}$得到F=$\frac{2\sqrt{10}}{3}$，BF=3，根据勾股定理得到AD²=DF²+AF²=$\frac{616}{9}$，DM=$\sqrt{B{D}^{2}-A{M}^{2}}$=$\frac{16}{3}$根据射影定理得到AD²=DM•DD′，于是得到结果．

解答 解：过A作AM⊥BC于M，过C作CE⊥AB于E，过D作DF⊥AB于F，
设AE=x，
由勾股定理得；AC²-AE²=BC²-BE²，
即7²-x²=6²-（11-x）²，
解得：x=$\frac{67}{11}$，
∴AE=$\frac{67}{11}$，BE=$\frac{54}{11}$，
∴CE=$\sqrt{A{C}^{2}-A{E}^{2}}$=$\frac{12\sqrt{10}}{11}$，
∵S_△ABC=$\frac{1}{2}$AM•BC=$\frac{1}{2}$AB•CE，
∴AM=2$\sqrt{10}$，
∵AD平分∠CAB，
∴$\frac{CD}{BD}=\frac{AC}{AB}=\frac{7}{11}$，
∵CD+BD=BC=6，
∴CD=$\frac{7}{3}$，BD=$\frac{11}{3}$，
∵CE⊥AB，DF⊥AB，
∴DF∥CE，
∴△BDF∽△BCE，
∴$\frac{BD}{BC}=\frac{DF}{CE}=\frac{BF}{BE}$，
∴DF=$\frac{2\sqrt{10}}{3}$，BF=3，
∴AD²=DF²+AF²=$\frac{616}{9}$，DM=$\sqrt{B{D}^{2}-A{M}^{2}}$=$\frac{16}{3}$，
∵AD、AD′是内、外角平分线，
∴∠D′AD=90°，
∵AM⊥DD′，
∴AD²=DM•DD′，
∴DD′=$\frac{616}{9}$×$\frac{3}{16}$=$\frac{77}{6}$．

点评 本题考查了角平分线性质，角平分线定理，勾股定理，射影定理，三角形的面积的应用，能求出△ADB的高是解此题的关键．