题目内容
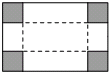如图是一块矩形铁皮，将四个角各剪去一个边长为2米的正方形后（剩下的部分做成一个）容积为90立方米的无盖长方体箱子，已知长方体箱子底面积的长比宽多4米，求矩形铁皮的面积．考点：一元二次方程的应用
专题：几何图形问题
分析：设矩形铁皮的宽为x米，则长为（x+4）米，无盖长方体箱子的底面长为（x+4-4）米，底面宽为（x-4）米，根据运输箱的容积为90立方米建立方程求出其解即可．
解答：解：设矩形铁皮的宽为x米，则长为（x+4）米，由题意，得
x（x-4）×2=90，
解得：x1=9，x2=-5（舍去），
所以矩形铁皮的长为：9+4=13米，
矩形铁皮的面积是：14×9=126（平方米）．
答：矩形铁皮的面积是126平方米．
x（x-4）×2=90，
解得：x1=9，x2=-5（舍去），
所以矩形铁皮的长为：9+4=13米，
矩形铁皮的面积是：14×9=126（平方米）．
答：矩形铁皮的面积是126平方米．
点评：本题考查了长方体的体积公式的运用，矩形的面积公式的运用，列一元二次方程解实际问题的运用，解答时由无盖长方体箱子的容积为90立方米建立方程是关键．
练习册系列答案
相关题目
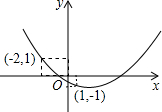如图，二次函数y=ax2+bx+c的图象经过点（1，-1）和（-2，1），下列关于此二次函数的叙述，正确的是（ ）| A、当x=0时，y的值小于-1 |
| B、当x=-3时，y的值大于1 |
| C、当x=5时，y的值等于0 |
| D、当x=1时，y的值大于1 |
下列运算正确的是（ ）
| A、x3+x2=x5 |
| B、（-x2）3=x6 |
| C、（-2x3）2=4x5 |
| D、（-x2）×（-x）3=x5 |
一条直线y=kx+b，其中k＞0，b＞0，那么该直线经过（ ）
| A、第一、二、三象限 |
| B、第一、二、四象限 |
| C、第一、三、四象限 |
| D、第二、三、四象限 |
若反比例函数y=
经过点（a，2a），a≠0，则此反比例函数的图象在（ ）
| k |
| x |
| A、第一、三象限 |
| B、第一、二象限 |
| C、第二、三象限 |
| D、第二、四象限 |