题目内容
在平面直角坐标系中，已知点E（-4，2），F（-2，-2），以原点O为位似中心，相似比为2，把△EFO放大，则点E的对应点E′的坐标是 ．
考点：位似变换,坐标与图形性质
专题：
分析：由在平面直角坐标系中，已知点E（-4，2），F（-2，-2），以原点O为位似中心，相似比为2，把△EFO放大，根据位似图形的性质，即可求得点E的对应点E′的坐标．
解答：解：∵点E（-4，2），以原点O为位似中心，相似比为2，把△EFO放大，
∴点E的对应点E′的坐标是：（-8，4）或（8，-4）．
故答案为：（-8，4）或（8，-4）．
∴点E的对应点E′的坐标是：（-8，4）或（8，-4）．
故答案为：（-8，4）或（8，-4）．
点评：此题考查了位似图形的性质．此题比较简单，注意位似图形有两个．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
下列各图形中，其中的一个三角形是由另一个三角形通过平移得到的是（ ）
A、 |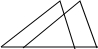
B、 |
C、 |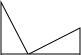
D、 |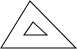
观察如图所示的长方形．下列等式变形中不一定正确的是（ ）
| A、如果a=b，那么a+2b=3b |
| B、如果a=b，那么a-m=b-m |
| C、如果a=b，那么ac2=bc2 |
| D、如果ac=bc，那么a=b |
已知一次函数y=kx+b，当0≤x≤2时，对应的函数值y的取值范围是-2≤y≤4，则k的值为（ ）
| A、3 | B、-3 |
| C、3或-3 | D、k的值不确定 |
如图，点B1是边长为1的等边△OBA的两条中线的交点，以OB1为一边，构造等边△OB1A1（点O，B1，A1按逆时针方向排列），称为第一次构造；点B2是△OB1A1的两条中线的交点，再以OB2为一边．构造等边△OB2A2（点O，B2，A2按逆时针方向排列），称为第二次构造；以此类推，…