题目内容
14．
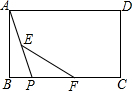如图，矩形ABCD中，点P从点B出发沿BC向点C运动，E、F分别是AP、PC的中点，则EF的长度（ ）| A． | 逐渐增大 | B． | 逐渐减小 | C． | 不变 | D． | 无法确定 |
分析 连接AC，根据勾股定理可求出AC的长，再根据三角形的中位线平行于第三边并且等于第三边的一半可得EF=$\frac{1}{2}$AC是一定值，问题得解．
解答 解：连接AC，
∵四边形ABCD是矩形，
∴∠D=90°，
∴AC=$\sqrt{A{D}^{2}+C{D}^{2}}$，
∵E、F分别是AP、PC的中点，
∴EF是△APC中位线，
∴EF=$\frac{1}{2}$AC为定值，
即EF的长度不变，
故选C
点评 本题考查了三角形的中位线平行于第三边并且等于第三边的一半，勾股定理，熟记定理和矩形的性质是解题的关键．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
如图，在△ABC中，AB=4，AC=3，BC=5，△ABD、△ACE、△BCF都是等边三角形，则四边形AEFD的面积为6．
6．∑表示数学中的求和符号，主要用于求多个数的和，∑下面的小字，i=1表示从1开始求和；上面的小字，如n表示求和到n为止．即$\sum_{i=1}^{n}$xi=x1+x2+x3+…+xn．则$\sum_{i=1}^{n}$（i2-1）表示（ ）
| A． | n2-1 | B． | 12+22+32+…+n2-（1+2+3+…+n ） | ||
| C． | 12+22+32+…+n2-n | D． | 12+22+32+…+i2-i |