题目内容
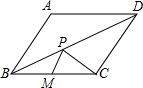如图，四边形ABCD是菱形，∠ABC=60°，M是BC的中点，CM=2．点P是BD上一动点，则PM+PC的最小值考点：菱形的性质,轴对称-最短路线问题
专题：
分析：根据菱形的性质，点A、C关于BD对称，连接AM即为PM+PC的最小值，再判断出△ABM是直角三角形，然后根据解直角三角形求出AM即可．
解答：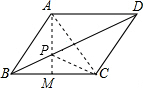
解：如图，∵四边形ABCD是菱形，
∴点A、C关于BD对称，
连接AM，AM即为PM+PC的最小值，
∵M是BC的中点，CM=2，
∴AB=BC=2×2=4，
∵∠ABC=60°，
∴△ABC是等边三角形，
∴△ABM是直角三角形，
∴AM=
AB=
×4=2
，
即PM+PC的最小值．
故答案为：2
．
解：如图，∵四边形ABCD是菱形，∴点A、C关于BD对称，
连接AM，AM即为PM+PC的最小值，
∵M是BC的中点，CM=2，
∴AB=BC=2×2=4，
∵∠ABC=60°，
∴△ABC是等边三角形，
∴△ABM是直角三角形，
∴AM=
| ||
| 2 |
| ||
| 2 |
| 3 |
即PM+PC的最小值．
故答案为：2
| 3 |
点评：本题考查了菱形的性质，等边三角形的判定与性质，轴对称确定最短路线问题，熟记各性质并确定出PM+PC的最小值的点P的位置是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
对于比较两个有理数的大小，下列四个说法：①倒数大的反而小；②绝对值大的反而小；③平方大的数则较大；④把两数求商，若商大于1，则被除数较大；商等于1，则两数相等；商小于1，则除数较大．其中说法正确的个数是（ ）
| A、4个 | B、2个 | C、1个 | D、0个 |
有理数m、n在数轴上所对应的店的位置如图所示，则m，n，-m，-n，1，-1的大小关系用“＞”表示为近似数27.38亿是精确到（ ）
| A、百分位 | B、百万位 |
| C、千万位 | D、亿位 |