题目内容
已知在△ABC中,D、E、F分别是BC、AC、AB的中点,AH⊥BC于H,若FD=8,求HE的长.
考点:三角形中位线定理,直角三角形斜边上的中线
专题:
分析:根据三角形中位线定理可得FD=
AC,进而得到AC=16,再根据直角三角形的性质:在直角三角形中,斜边上的中线等于斜边的一半可得答案.
| 1 |
| 2 |
解答: 解:∵D、F分别是BC、AB的中点,
解:∵D、F分别是BC、AB的中点,
∴FD=
AC,
∵FD=8,
∴AC=16,
∵AH⊥BC于H,
∴∠AHC=90°,
∵E是AC中点,
∴HE=
AC=8.
 解:∵D、F分别是BC、AB的中点,
解:∵D、F分别是BC、AB的中点,∴FD=
| 1 |
| 2 |
∵FD=8,
∴AC=16,
∵AH⊥BC于H,
∴∠AHC=90°,
∵E是AC中点,
∴HE=
| 1 |
| 2 |
点评:此题主要考查了三角形中位线定理,以及直角三角形的性质,关键是掌握三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
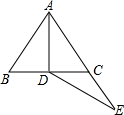 如图,已知等边三角形ABC中,AD是BC边上中线,E是AC延长线上一点,且CE=CD,AD=
如图,已知等边三角形ABC中,AD是BC边上中线,E是AC延长线上一点,且CE=CD,AD=