题目内容
7.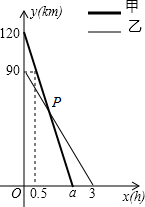 在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.设甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,请回答下列问题:
在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.设甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,请回答下列问题:(1)A、C两村间的距离为120km,a=2;
(2)求出甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系式,并求出图中点P的坐标;
(3)乙在行驶过程中,何时距甲10km?
分析 (1)由图可知与y轴交点的坐标表示A、C两村间的距离为120km,再由0.5小时距离C村90km,行驶120-90=30km,速度为60km/h,求得a=2;
(2)求得y1,y2两个函数解析式,建立方程即可求得点P坐标;
(3)由(2)中的函数解析式,根据距甲10km建立方程,探讨得出答案即可.
解答 解:(1)A、C两村间的距离120km,
a=120÷[(120-90)÷0.5]=2;
故答案为:120,2;
(2)设y1=k1x+120,
代入(2,0)得:0=2k1+120,
解得:k1=-60,
所以y1=-60x+120,
设y2=k2x+90,
代入(3,0)得:0=3k2+90,
解得:k2=-30,
所以y2=-30x+90,
由-60x+120=-30x+90
解得x=1,则y1=y2=60,
所以P(1,60);
(3)当y1-y2=10,
即-60x+120-(-30x+90)=10,
解得x=$\frac{2}{3}$,
当y2-y1=10,
即-30x+90-(-60x+120)=10,
解得x=$\frac{4}{3}$,
当甲走到C地,而乙距离C地10km时,
-30x+90=10,
解得x=$\frac{8}{3}$;
综上所知当x=$\frac{2}{3}$h,或x=$\frac{4}{3}$h,或x=$\frac{8}{3}$h乙距甲10km.
点评 此题考查一次函数的运用,一次函数与二元一次方程组的运用,解题的关键是认真分析图象求出解析式,并且注意分类思想的运用.

练习册系列答案
 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
18.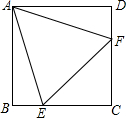 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④AD=$\sqrt{3}$,其中正确的结论个数为( )
如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④AD=$\sqrt{3}$,其中正确的结论个数为( )
 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④AD=$\sqrt{3}$,其中正确的结论个数为( )
如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④AD=$\sqrt{3}$,其中正确的结论个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.下列调查中,最适合采用抽样调查方式的是( )
| A. | 值日老师调查各班学生的出勤情况 | |
| B. | 调查凉山州中学生参加体育锻炼的时间 | |
| C. | 了解某班女学生的身高情况 | |
| D. | 了解全班同学的课外读书时间 |
 如图,在⊙O中,$\widehat{AB}$=$\widehat{CD}$,∠DCB=28°,则∠ABC=28度.
如图,在⊙O中,$\widehat{AB}$=$\widehat{CD}$,∠DCB=28°,则∠ABC=28度. 如图,△ABC是等腰直角三角形,∠C=90°,点D是AB的中点,点P是AB上的一个动点(点P与点A、B不重合),矩形PECF的顶点E,F分别在BC,AC上.
如图,△ABC是等腰直角三角形,∠C=90°,点D是AB的中点,点P是AB上的一个动点(点P与点A、B不重合),矩形PECF的顶点E,F分别在BC,AC上. 如图,在Rt△ABC中,∠A=90°,BD平分∠ABC交AC于D点,AB=4,BD=5,点P是线段BC上的一动点,则PD的最小值是3.
如图,在Rt△ABC中,∠A=90°,BD平分∠ABC交AC于D点,AB=4,BD=5,点P是线段BC上的一动点,则PD的最小值是3. 如图,已知△ABC≌△ADE,若AB=7,AC=3,则BE的值为4.
如图,已知△ABC≌△ADE,若AB=7,AC=3,则BE的值为4.