题目内容
20. 如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO、BO的中点.若AC+BD=24cm,EF的长为3cm,则△OAB的周长是( )
如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO、BO的中点.若AC+BD=24cm,EF的长为3cm,则△OAB的周长是( )| A. | 16cm | B. | 18cm | C. | 20cm | D. | 22cm |
分析 根据平行四边形的性质可知OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD,求出OB+OA=12cm,由三角形中位线定理求出AB的长,即可得出△OAB的周长.
解答 解:∵?ABCD的对角线AC,BD相交于点O,
∴OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD
∵AC+BD=24cm,
∴OB+0A=12cm,
∵点E,F分别是线段AO,BO的中点,
∴AB=2EF=6cm,
∴△OAB的周长=OA+OB+AB=12+6=18(cm);
故选:C.
点评 本题主要考查了三角形中位线定理以及平行四边形的性质;熟练掌握平行四边形的性质,求出AB的长是解决问题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
15.如表是我市4个区县今年5月31日最高气温(℃)的统计结果:
该日最高气温的众数和中位数分别是( )
| 永定区 | 武陵源区 | 慈利县 | 桑植县 |
| 32 | 32 | 33 | 30 |
| A. | 32℃,32℃ | B. | 32℃,33℃ | C. | 33℃,33℃ | D. | 32℃,30℃ |
15.反比例函数y=-$\frac{3}{x}$的图象上有P1(x1,-2),P2(x2,-3)两点,则x1与x2的大小关系是( )
| A. | x1>x2 | B. | x1=x2 | C. | x1<x2 | D. | 不确定 |
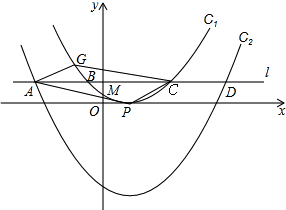
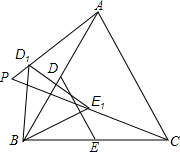 已知:在等边△ABC中,AB=2$\sqrt{3}$,D、E分别是AB,BC的中点(如图),若将△BDE绕点B逆时针旋转,得到△BD1E1.设旋转的角为α(0°<α<180°),记射线CE1与AD1的交点为P,点P到BC所在直线的距离的最大值为2.
已知:在等边△ABC中,AB=2$\sqrt{3}$,D、E分别是AB,BC的中点(如图),若将△BDE绕点B逆时针旋转,得到△BD1E1.设旋转的角为α(0°<α<180°),记射线CE1与AD1的交点为P,点P到BC所在直线的距离的最大值为2.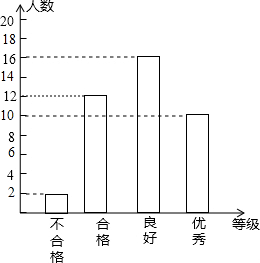 为了提高教师的综合素质,教育部门对全长沙市教师进行某项专业技能培训.为了解培训的效果,培训结束后随机抽取了部分参训老师进行技能测试,测试结果分成“不合格”、“合格”、“良好”、“优秀”四个等级,并绘制了如图所示的统计图,请根据统计图提供的信息,回答下列问题:
为了提高教师的综合素质,教育部门对全长沙市教师进行某项专业技能培训.为了解培训的效果,培训结束后随机抽取了部分参训老师进行技能测试,测试结果分成“不合格”、“合格”、“良好”、“优秀”四个等级,并绘制了如图所示的统计图,请根据统计图提供的信息,回答下列问题: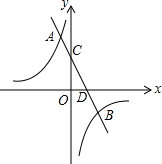 如图,在平面直角坐标系xOy中,一次函数y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$的图象交于点A(-1,6)和点B(3,m),与y轴交于点C,与x轴交于点D.
如图,在平面直角坐标系xOy中,一次函数y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$的图象交于点A(-1,6)和点B(3,m),与y轴交于点C,与x轴交于点D.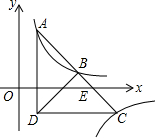 如图,Rt△ADC在平面直角坐标系下如图放置,斜边AC交x轴于点E,过点A的双曲线y=$\frac{k}{x}$(m≠0)交Rt△ADC斜边AC的中点B,连接BD,过点C作双曲线y=$\frac{m}{x}$(m≠0).若BD=3BE,A的坐标为(1,8),则m=( )
如图,Rt△ADC在平面直角坐标系下如图放置,斜边AC交x轴于点E,过点A的双曲线y=$\frac{k}{x}$(m≠0)交Rt△ADC斜边AC的中点B,连接BD,过点C作双曲线y=$\frac{m}{x}$(m≠0).若BD=3BE,A的坐标为(1,8),则m=( )