题目内容
3．已知x2+mx-4在整数范围内可以因式分解，求自然数m的值，并把它们分解因式．分析 把-4分成4和-1，-4和1，2和-2，-2和2，然后根据“x2+（p+q）x+pq”型的式子的因式分解．
解答 解：当x2+mx-4=（x+4）（x-1）时，m=4+（-1）=3，
当x2+mx-4=（x-4）（x+1）时，m=-4+1=-3，
当x2+mx-4=（x+2）（x-2）时，m=2+（-2）=0，
当x2+mx-4=（x-2）（x+2）时，m=-2+2=0．
点评 本题主要考查对因式分解-十字相乘法的理解和掌握，理解x2+（a+b）x+ab=（x+a）（x+b）是解此题的关键．
练习册系列答案
相关题目
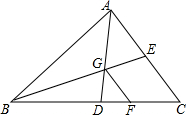如图，已知点G为△ABC的重心，GF∥AC，求DF：FC、BC：BF的值．
已知AB∥DE，BF、DF分别平分∠ABC，∠CDE，求∠C、∠F的关系．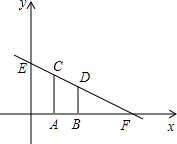
在平面直角坐标系中，CA⊥x轴于点A（1，0），BD⊥x轴于点B（3，0），直线CD与x轴，y轴分别交于点F，E，且解析式y=kx+3，S四边形ABCD=4，求直线CD的解析式．
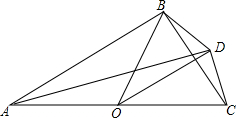如图，OA=OB=OD=OC=3，且∠BAD=15°，则S△BOD=$\frac{9}{4}$．