题目内容
13.(1)解不等式组:$\left\{\begin{array}{l}{2(x+2)≤3x+3}\\{\frac{x}{3}<\frac{x+1}{4}}\end{array}\right.$(2)解方程:$\frac{3}{x-1}$=$\frac{2}{x+1}$.
分析 (1)分别求出各不等式的解集,再求出其公共解集;
(2)先把分式方程化为整式方程,求出x的值代入原分式方程的公分母进行检验即可.
解答 解:(1)$\left\{\begin{array}{l}{2(x+2)≤3x+3①}\\{\frac{x}{3}<\frac{x+1}{4}②}\end{array}\right.$,
由①得,x≥1;
由②得,x<3,
故此不等式组的解集为:1≤x<3;
(2)原方程可化为:3(x+1)-2(x-1)=0,
解得x=-5,
把x=-5代入(x-1)(x+1)≠0.
故x=-5是原分式方程的解.
点评 本题考查的是解一元一次不等式组和分式方程,熟知解一元一次不等式的基本步骤和解分式方程的步骤是解答此题的关键.

练习册系列答案
相关题目
4. 如图,直线a,b被直线c所截,则图中与∠1是同位角的是( )
如图,直线a,b被直线c所截,则图中与∠1是同位角的是( )
 如图,直线a,b被直线c所截,则图中与∠1是同位角的是( )
如图,直线a,b被直线c所截,则图中与∠1是同位角的是( )| A. | ∠2 | B. | ∠3 | C. | ∠4 | D. | ∠5 |
8.下列各数中,属于无理数的是( )
| A. | -2 | B. | $\frac{22}{7}$ | C. | $\sqrt{3}$ | D. | 0.101001000 |
18.下列函数中,y是x的反比例函数有( )
(1)y=3x;(2)y=-$\frac{2}{x}$;(3)$y=\frac{x}{3}$;(4)-xy=3;(5)$y=\frac{2}{x+1}$;(6)$y=\frac{1}{x^2}$;(7)y=2x-2;(8)$y=\frac{k}{x}$.
(1)y=3x;(2)y=-$\frac{2}{x}$;(3)$y=\frac{x}{3}$;(4)-xy=3;(5)$y=\frac{2}{x+1}$;(6)$y=\frac{1}{x^2}$;(7)y=2x-2;(8)$y=\frac{k}{x}$.
| A. | (2)(4) | B. | (2)(3)(5)(8) | C. | (2)(7)(8) | D. | (1)(3)(4)(6) |
3.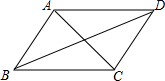 如图,在平行四边形ABCD中,连接对角线AC、BD,图中的全等三角形的对数( )
如图,在平行四边形ABCD中,连接对角线AC、BD,图中的全等三角形的对数( )
 如图,在平行四边形ABCD中,连接对角线AC、BD,图中的全等三角形的对数( )
如图,在平行四边形ABCD中,连接对角线AC、BD,图中的全等三角形的对数( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
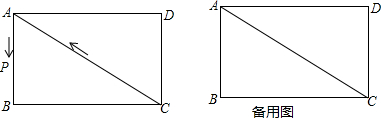
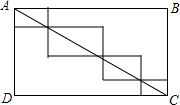 如图,长方形ABCD的边AB=7,BC=4,则图中四个小长方形的周长之和为22.
如图,长方形ABCD的边AB=7,BC=4,则图中四个小长方形的周长之和为22.