题目内容
2.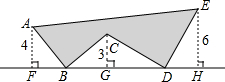 如图,AB=BC,CD=DE,AB⊥BC,CD⊥DE,AF⊥FH,CG⊥FH,EH⊥FH,AF=4,CG=3,EH=6,阴影部分面积为50.
如图,AB=BC,CD=DE,AB⊥BC,CD⊥DE,AF⊥FH,CG⊥FH,EH⊥FH,AF=4,CG=3,EH=6,阴影部分面积为50.
分析 根据垂直的定义得到∠ABC=∠AFB=∠BGC=90°,由余角的性质得到∠FAB=∠CBG,推出△ABF≌△BCG,根据全等三角形的性质得到BF=CG=3,AF=BG=4,同理△DCG≌△EDH,根据全等三角形的性质得到DG=EH=6,DH=CG=3,于是得到FH=BF+BG+DG+DH=16,BD=BG+DG=10,即可得到结论.
解答 解:∵AB⊥BC,AF⊥FH,CG⊥FH,
∴∠ABC=∠AFB=∠BGC=90°,
∴∠FAB+∠ABF=∠ABF+∠CBG=90°,
∴∠FAB=∠CBG,
在△AFB与△BCG中,
$\left\{\begin{array}{l}{∠AFB=∠BGC}\\{∠FAB=∠CBG}\\{∠AB=BC}\end{array}\right.$,
∴△ABF≌△BCG,
∴BF=CG=3,AF=BG=4,
同理:△DCG≌△EDH,
∴DG=EH=6,DH=CG=3,
∴FH=BF+BG+DG+DH=16,BD=BG+DG=10,
∴S阴影=S梯形AFHE-S△ABF-S△BDC-S△DEH=$\frac{1}{2}$(4+6)×16-$\frac{1}{2}×3×4$-$\frac{1}{2}×10×3$-$\frac{1}{2}×3×6$=50.
故答案为:50.
点评 本题考查了全等三角形的判定和性质,梯形的面积三角形的面积,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
7.下面两个三角形一定相似的是( )
| A. | 两个等边三角形 | B. | 两个等腰三角形 | C. | 两个直角三角形 | D. | 两个锐角三角形 |
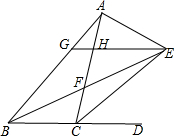 如图,△ABC的内角∠ABC和外角∠ACD的平分线交于点E,BE交AC于点F,过点E作EG∥BD交AB于点G,交AC于点H,连接AE,以下结论:
如图,△ABC的内角∠ABC和外角∠ACD的平分线交于点E,BE交AC于点F,过点E作EG∥BD交AB于点G,交AC于点H,连接AE,以下结论: