题目内容
11.在一个不透明的盒子里装有5个分别写有数字-2,-1,1,2,3的小球,它们除数字不同外其余全部相同,现从盒子里随机取出一个小球,将该小球上的数字作为点P的横坐标,将该数的绝对值作为点P的纵坐标,则点P落在抛物线y=-x2+2x+4与x轴所围成的区域内(不含边界)的概率是$\frac{2}{5}$.分析 首先根据题意求得所有的点P的坐标,然后求得二次函数与x轴的交点与顶点坐标,画出图象;然后分别分析在抛物线y=-x2+2x+4与x轴所围成的区域内(不含边界)的情况,再利用概率公式求解即可求得答案.
解答 解:如图,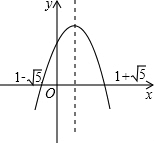 -2,-1,1,2,3的绝对值为2,1,1,2,3.
-2,-1,1,2,3的绝对值为2,1,1,2,3.
点P的坐标为(-2,2),(-1,1),(1,1),(2,2),(3,3);
描出各点:-2<1-$\sqrt{5}$,不合题意;
把x=-1代入解析式得:y1=1,1=1,故(-1,1)在边界上,不在区域内;
把x=1代入解析式得:y2=5,1<5,故(1,1)在该区域内;
把x=2代入解析式得:y3=4,2<4,故(2,2)在该区域内;
把x=3代入解析式得:y4=1,1<3,故(3,3)不在该区域内.
所以5个点中有2个符合题意.
故点P落在抛物线y=-x2+2x+4与x轴所围成的区域内(不含边界)的概率是$\frac{2}{5}$.
故答案为:$\frac{2}{5}$.
点评 此题考查了二次函数的性质,概率公式的应用以及绝对值的定义.此题难度适中,解题的关键是注意数形结合思想的应用.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
19.两条直线相交可以形成2对对顶角,那么同一平面内4条直线最多可以形成对顶角( )
| A. | 8对 | B. | 10对 | C. | 12对 | D. | 16对 |
20.泗阳华润苏果超市准备购进A、B两种品牌的书包共100个,已知两种书包的进价如下表所示,设购进A种书包x个,且所购进的两种书包能全部卖出,获得的总利润为y元.
(1)将表格的信息填写完整;
(2)求y关于x的函数表达式;
(3)如果购进两种书包的总费用不超过4500元且购进B种书包的数量不大于A种书包的3倍,那么超市如何进货才能获利最大?并求出最大利润.
| 品牌 | 购买个数(个) | 进价(元/个) | 售价(元/个) | 获利(元) |
| A | x | 50 | 60 | 10x |
| B | 100-x | 40 | 55 | 15(100-x) |
(2)求y关于x的函数表达式;
(3)如果购进两种书包的总费用不超过4500元且购进B种书包的数量不大于A种书包的3倍,那么超市如何进货才能获利最大?并求出最大利润.
1.服装店销售某款服装,每件服装的标价为300元,若按标价的八折销售,仍可获利60元,则这款服装每件的标价比进价多( )
| A. | 60元 | B. | 80元 | C. | 120元 | D. | 180元 |