题目内容
15.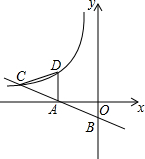 如图,直线y=-$\frac{1}{2}$x-1与x轴、y轴分别交于点A、B,与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点C,过点A作AD⊥0A,交反比例函数的图象于点D,连结CD.
如图,直线y=-$\frac{1}{2}$x-1与x轴、y轴分别交于点A、B,与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点C,过点A作AD⊥0A,交反比例函数的图象于点D,连结CD.(1)若已知AB=AC,求反比例函数的表达式;
(2)若已知CD=AC,求△ACD的面积.
分析 (1)作CE⊥x轴于E,根据直线的解析式求出点A、B的坐标,得到OA、OB的长,证明△ACE≌△AOB,确定点C的坐标求出反比例函数的表达式;
(2)作CF⊥AD于F,根据等腰山脚下的性质和已知得到点C的坐标,求出△ACD的面积.
解答 解:(1)作CE⊥x轴于E,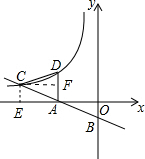
直线y=-$\frac{1}{2}$x-1与x轴、y轴分别交于点A(-2,0)、B(0,-1),
在△ACE和△AOB中
$\left\{\begin{array}{l}{∠CAE=∠BAO}\\{∠CEA=∠BOA}\\{AC=AB}\end{array}\right.$,
∴△ACE≌△AOB,
∴CE=OB=1,AE=OA=2,
∴C(-4,1)
∴反比例函数的表达式为:y=-$\frac{4}{x}$;
(2)作CF⊥AD于F,
∵CD=AC,∴点F为AD的中点,
∴D(-2,-$\frac{k}{2}$),F(-2,-$\frac{k}{4}$),
∴C($\frac{k}{2}$-2,-$\frac{k}{4}$),
则($\frac{k}{2}$-2)×(-$\frac{k}{4}$)=k,
解得,k=-4,
∴△ACD的面积=$\frac{1}{2}$×AD×CF=2.
点评 本题考查的是一次函数与反比例函数的交点问题,能够求出直线与坐标轴的交点和直线与双曲线的交点是解题的关键,注意数形结合思想的运用.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
3. 如图,将矩形ABCO放在直角坐标系中,其中顶点B的坐标为(10,8),E是BC边上一点,将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=$\frac{k}{x}$的图象与边AB交于点F,则线段AF的长为( )
如图,将矩形ABCO放在直角坐标系中,其中顶点B的坐标为(10,8),E是BC边上一点,将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=$\frac{k}{x}$的图象与边AB交于点F,则线段AF的长为( )
 如图,将矩形ABCO放在直角坐标系中,其中顶点B的坐标为(10,8),E是BC边上一点,将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=$\frac{k}{x}$的图象与边AB交于点F,则线段AF的长为( )
如图,将矩形ABCO放在直角坐标系中,其中顶点B的坐标为(10,8),E是BC边上一点,将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=$\frac{k}{x}$的图象与边AB交于点F,则线段AF的长为( )| A. | $\frac{15}{4}$ | B. | 2 | C. | $\frac{15}{8}$ | D. | $\frac{3}{2}$ |
7.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. | 矩形 | B. | 平行四边形 | C. | 等腰三角形 | D. | 直角三角形 |
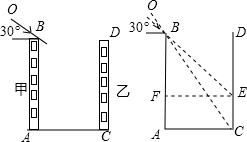 棕北中学暑假期间将进行校园外貌环境改造.如图为校园内的两幢教学楼,它们的高AB=CD=35m,它们之间的水平距离AC=30m,现工人现需了解甲楼对乙楼的采光的影响情况,当太阳光与水平线的夹角为30°角时,求EC的高度.
棕北中学暑假期间将进行校园外貌环境改造.如图为校园内的两幢教学楼,它们的高AB=CD=35m,它们之间的水平距离AC=30m,现工人现需了解甲楼对乙楼的采光的影响情况,当太阳光与水平线的夹角为30°角时,求EC的高度. 如图所示,AB⊥AD,BC⊥CD,∠B=3∠D,求∠B、∠D的度数.
如图所示,AB⊥AD,BC⊥CD,∠B=3∠D,求∠B、∠D的度数.