题目内容
2. 如图,E,F是?ABCD的对角线AC上两点,且AE=CF,请你写出图中的一对全等三角形并对其进行证明.
如图,E,F是?ABCD的对角线AC上两点,且AE=CF,请你写出图中的一对全等三角形并对其进行证明.
分析 图中的相似三角形有:△ADE≌△CBF、△ABF≌△CDE、△ABC≌△CDA
解答 ①△ADE≌△CBF (或△ABF≌△CDE,△ABC≌△CDA)
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC
∴∠DAE=∠BCF
在△ADE 和△CBF中$\left\{\begin{array}{l}AD=CB\\∠DAE=∠BCF\\ AE=CF\end{array}\right.$
∴△ADE≌△CBF (SAS)
②△ABF≌△CDE
证明:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC
∴∠BAF=∠DCE
∵AE=CF,
∴AE+EF=CF+EF,
∴AF=CE
在△ABF 和△CDE中,$\left\{\begin{array}{l}{AB=CD}\\{∠BAF=∠DCA}\\{AF=CE}\end{array}\right.$
∴△ABF≌△CDE(SAS)
③△ABC≌△CDA
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥DC,
∴∠BAC=∠DCA,
在△ABC与△CDA中,$\left\{\begin{array}{l}{∠BAC=∠DCA}\\{AC=CA}\\{∠BCA=∠CAD}\end{array}\right.$,
∴△ABC≌△CDA(ASA)
注:学生答三种情况之一即可.
点评 本题考查了平行四边形的性质及全等三角形的判定,解题的关键是熟悉全等三角形的判定定理与平行四边形的性质.

练习册系列答案
相关题目
12.平移边长为1的小菱形◇可以得到美丽的“中国结”图案.下面四个图案是由◇平移后得到的类似“中国结”的图案,其中第(1)个图形含边长为1的菱形2个,第(2)个图形含边长为1的菱形8个,第(3)个图形含边长为1的菱形18个,则第(6)个图形中含边长为1的菱形的个数是( )
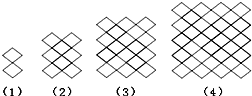

| A. | 32 | B. | 36 | C. | 50 | D. | 72 |
13.不等式$\frac{1}{3}$(x-m)>3-m的解集为x>1,则m的值为( )
| A. | 1 | B. | -1 | C. | 4 | D. | -4 |
10.函数y=2x-5的图象经过( )
| A. | 第一、三、四象限 | B. | 第一、二、四象限 | C. | 第二、三、四象限 | D. | 第一、二、三象限 |
17. 如图,在Rt△ACB中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D,则图中的全等三角形对数共有( )
如图,在Rt△ACB中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D,则图中的全等三角形对数共有( )
 如图,在Rt△ACB中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D,则图中的全等三角形对数共有( )
如图,在Rt△ACB中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D,则图中的全等三角形对数共有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
14.陈文住在学校的正东200米处,从陈文家出发向北走150米就到了李明家,若选取李明家为原点,分布以正东、正北方向为x轴、y轴正方向建立平面直角坐标系,则学校的坐标是( )
| A. | (150,200) | B. | (200,150) | C. | (-150,-200) | D. | (-200,-150) |
11.已知点(-1,y1),B(1,y2)都在直线y=-4x+3上,则y1,y2大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能比较 |
12.“十是十,四是四,十四是十四,四十是四十”,在这句含有16个汉字的绕口令中,“十”出现的频率为( )
| A. | $\frac{1}{4}$ | B. | 4 | C. | 6 | D. | $\frac{3}{8}$ |
 如图,△ABF≌△DCE,点B,E,F,C在同一直线上,已知∠A=∠D,∠B=∠C,若BF=5,EF=3,则CF=2.
如图,△ABF≌△DCE,点B,E,F,C在同一直线上,已知∠A=∠D,∠B=∠C,若BF=5,EF=3,则CF=2.