题目内容
5.先阅读下面的材料,然后解答问题.通过计算,发现:方程x+$\frac{1}{x}$=2+$\frac{1}{2}$的解为x1=2,x2=$\frac{1}{2}$;方程x+$\frac{1}{x}$=3+$\frac{1}{3}$的解为x1=3,x2=$\frac{1}{3}$;方程x+$\frac{1}{x}$=4+$\frac{1}{4}$的解为x1=4,x2=$\frac{1}{4}$;…
(1)观察猜想:关于x的方程x+$\frac{1}{x}$=n+$\frac{1}{n}$的解是x1=n,x2=$\frac{1}{n}$;
(2)实践运用:对于关于x的方程x-$\frac{1}{x}$=m-$\frac{1}{m}$的解,小明观察得“x=m”是该方程的一个解,请你猜想该方程的另一个解,并用方程的解的概念对该解进行验证;
(3)拓展延伸:请利用上面的规律,求关于x的方程x+$\frac{1}{x-3}$=a+$\frac{1}{a-3}$的解.
分析 根据例题可以得到:方程的左边与右边的式子形式完全相同,只是左边是未知数,右边是把未知数换成了具体的数,则方程的解是方程右边的两部分,据此即可求解.
解答 解:(1)根据上面的规律,猜想关于x的方程$x+\frac{1}{x}$=$n+\frac{1}{n}$的解是 x1=n,x2=$\frac{1}{n}$;
故答案为:x1=n,x2=$\frac{1}{n}$.
(2)类似的,关于x的方程x-$\frac{1}{x}$=m-$\frac{1}{m}$的解是 x1=m,x2=-$\frac{1}{m}$;
(3)x+$\frac{1}{x-3}$=a+$\frac{1}{a-3}$,
可得:x-3+$\frac{1}{x-3}$=a-3+$\frac{1}{a-3}$,
可得:x1=a,x2=$\frac{1}{a-3}$+3=$\frac{3a-8}{a-3}$.
点评 本题考查分式方程的解,正确理解例题,发现方程与解之间的关系:方程的左边与右边的式子形式完全相同,只是左边是未知数,右边是把未知数换成了具体的数,则方程的解是方程右边的两部分,是解题的关键.

练习册系列答案
相关题目
13.若把分$\frac{2xy}{2x+y}$中的x和y都扩大3倍,那么分式的值( )
| A. | 扩大3倍 | B. | 不变 | C. | 缩小3倍 | D. | 扩大9倍 |
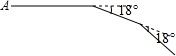 如图,小亮从A点出发前进10m,向右转18°,再前进10m,又向右转18°,…,这样一直走下去,他第一次回到出发点A时,一共走了200m.
如图,小亮从A点出发前进10m,向右转18°,再前进10m,又向右转18°,…,这样一直走下去,他第一次回到出发点A时,一共走了200m. 如图,反比例函数y=$\frac{k}{x}$的图象过面积为$\sqrt{2}$的矩形ABOC的顶点A,则k=-$\sqrt{2}$.
如图,反比例函数y=$\frac{k}{x}$的图象过面积为$\sqrt{2}$的矩形ABOC的顶点A,则k=-$\sqrt{2}$.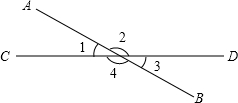 如图所示,AB与CD相交所成的四个角中,∠1的邻补角是∠2和∠4.
如图所示,AB与CD相交所成的四个角中,∠1的邻补角是∠2和∠4. 如图,矩形ABCD的对角线AC=8cm,∠AOD=120°,则AB的长为4cm.
如图,矩形ABCD的对角线AC=8cm,∠AOD=120°,则AB的长为4cm.