题目内容
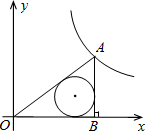
（2012•桐乡市三模）定义：定点A与⊙O上任意一点之间的距离的最小值称为点A与⊙O之间的距离．现有一矩形ABCD（如图），AB=14cm，BC=12cm，⊙K与矩形的边AB，BC，CD分别切于点E，F，G，则点A与⊙K的距离为（ ）A．4cm
B．8cm
C．10cm
D．12cm
【答案】分析：连接EK，AK，根据题目定义知道AH就是点A与⊙K的距离，由切线的性质，可求出EK=6cm，进而求出AE=8cm；由勾股定理求出AK=10cm，减去⊙K的半径即得距离．
解答：
解：连接KE，KF，KG、AK，交⊙K于H点，
∵ABCD是矩形，⊙K与矩形的边AB，BC，CD分别切于点E，F，G，
∴EK=FK=KG，
∴四边形BEKF、四边形FKGC均为正方形，
∴BF=FC=EK=6cm；
∵AB=14cm，
∴AE=8cm，AK=10cm，
∴AH=AK-KH=10-6=4cm，
∴点A与⊙K的距离为4cm．
故选A．
点评：此题主要考查学生对切线的性质及勾股定理的理解及运用．
解答：
解：连接KE，KF，KG、AK，交⊙K于H点，∵ABCD是矩形，⊙K与矩形的边AB，BC，CD分别切于点E，F，G，
∴EK=FK=KG，
∴四边形BEKF、四边形FKGC均为正方形，
∴BF=FC=EK=6cm；
∵AB=14cm，
∴AE=8cm，AK=10cm，
∴AH=AK-KH=10-6=4cm，
∴点A与⊙K的距离为4cm．
故选A．
点评：此题主要考查学生对切线的性质及勾股定理的理解及运用．
练习册系列答案
考前必练系列答案
相关题目
（2012•桐乡市三模）如图，点A（a，b）在双曲线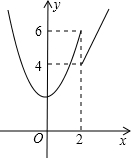
（2012•桐乡市三模）已知函数