Question

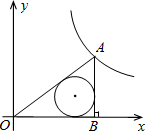（2012•桐乡市三模）如图，点A（a，b）在双曲线y=

k

x

(x＞0)上，AB⊥x轴于点B，若点P(5

3

， 4

3

)是双曲线上异于点A的另一点．
（1）k=

60

；
（2）若a²=169-b²，则△OAB的内切圆半径r=

2

．

Answer 1

分析：（1）把P点坐标代入反比例函数，即可求k；
（2）先把A点坐标代入反比例函数可得ab=60，再结合a²=169-b²组成方程组，解可得a、b的值，进而利用勾股定理可求OA，再结合直角三角形内切圆半径公式，易求r．

解答：解：（1）把（5

3

，4

3

）代入反比例函数，可得
k=5

3

×4

3

=60；

（2）把（a，b）代入反比例函数，得
ab=60与a²=169-b²联合组成方程组为：

ab=60 a2=169-b2

，
解得

a=12 b=5

或

a=5 b=12

，
即知OB=12，AB=5或OB=5，AB=12，
在Rt△AOB中，OA=13，
故△AOB内切圆的半径r=

a+b-c

2

=

5+12-13

2

=2．

点评：本题考查了反比例函数的知识、勾股定理，解题的关键是能根据所给的点，求出k，并能解二元二次方程组．