题目内容
2.某公司为了扩大生产规模,决定新购进6台机器,但所用资金不超过68万元,现有甲、乙两种机器可供选择,甲每台14万元,乙每台10万元,问该公司有哪几种购买方案,并说明理由.分析 首先设购进x台甲种机器,则购进乙种机器(6-x)台,根据关键语句“所用资金不超过68万元”可得不等式14x+10(6-x)≤68,再解不等式即可.
解答 解:设购进x台甲种机器,则购进乙种机器(6-x)台,由题意得:
则14x+10(6-x)≤68,
解之,得x≤2,
即0≤x≤2,
∴x=0,1,2,
所以共有3种方案,分别是:
方案1:全购进乙种机器6台;
方案2:购进1台甲种机器,则购进乙种机器5台;
方案3:购进2台甲种机器,则购进乙种机器4台.
点评 此题主要考查了一元一次不等式的应用,关键是正确理解题意,找出题目中的不等关系,列出不等式.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
13. 如图,已知∠1=∠2=∠3=55°,则∠4的度数是( )
如图,已知∠1=∠2=∠3=55°,则∠4的度数是( )
 如图,已知∠1=∠2=∠3=55°,则∠4的度数是( )
如图,已知∠1=∠2=∠3=55°,则∠4的度数是( )| A. | 55° | B. | 95° | C. | 115° | D. | 125° |
10.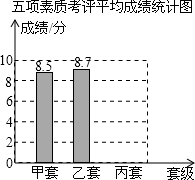 学校通过初评决定最后从甲、乙、丙三个班中推荐一个班为区级先进班集体,下表是这三个班的五项素质考评得分表.五项素质考评得分表(单位:分):
学校通过初评决定最后从甲、乙、丙三个班中推荐一个班为区级先进班集体,下表是这三个班的五项素质考评得分表.五项素质考评得分表(单位:分):
根据统计表中的信息解答下列问题:五项素质考评平均成绩统计图
(1)请你补全五项成绩考评分析表中的数据:五项成绩考评分析表:
(2)参照上表中的数据,你推荐哪个班为区级先进班集体?并说明理由.
(3)如果学校把行为规范、学习成绩、校运动会、艺术获奖、劳动卫生五项考评成绩按照3:2:1:1:3的比确定,学生处的李老师根据这个平均成绩,绘制一幅不完整的条形统计图,请将这个统计图补充完整,依照这个成绩,应推荐哪个班为区级先进班集体?
 学校通过初评决定最后从甲、乙、丙三个班中推荐一个班为区级先进班集体,下表是这三个班的五项素质考评得分表.五项素质考评得分表(单位:分):
学校通过初评决定最后从甲、乙、丙三个班中推荐一个班为区级先进班集体,下表是这三个班的五项素质考评得分表.五项素质考评得分表(单位:分):| 班级 | 行为规范 | 学习成绩 | 校运动会 | 艺术获奖 | 劳动卫生 |
| 甲班 | 10 | 10 | 6 | 10 | 7 |
| 乙班 | 10 | 8 | 8 | 9 | 8 |
| 丙班 | 9 | 10 | 9 | 6 | 9 |
(1)请你补全五项成绩考评分析表中的数据:五项成绩考评分析表:
| 班级 | 平均分 | 众数 | 中位数 |
| 甲班 | 8.6 | 10 | ③ |
| 乙班 | 8.6 | ② | 8 |
| 丙班 | ① | 9 | 9 |
(3)如果学校把行为规范、学习成绩、校运动会、艺术获奖、劳动卫生五项考评成绩按照3:2:1:1:3的比确定,学生处的李老师根据这个平均成绩,绘制一幅不完整的条形统计图,请将这个统计图补充完整,依照这个成绩,应推荐哪个班为区级先进班集体?
12.如图,∠1和∠2是同位角的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,在△ABC中,∠A=60°,∠B=45°,BC=$2\sqrt{2}$,求S△ABC的值.
如图,在△ABC中,∠A=60°,∠B=45°,BC=$2\sqrt{2}$,求S△ABC的值.