题目内容
19.(1)已知抛物线y=mx2+(3m-1)x-3与x轴交于两个不同的整数点,且m为正整数,试确定抛物线的解析式;(2)若点P(x1,k)与Q(x1+n,k)都在(1)中的抛物线上(点P,Q不重合),将抛物线在PQ下方的部分沿PQ翻折,抛物线的其它部分保持不变,得到一个新图象.当这个新图象与x轴恰好只有两个公共点时,求k的取值范围.
分析 (1)y=0,结合与x轴交于两个不同的整数点即可求出m的值;
(2)由题意判断PQ与x轴平行,结合翻折的性质进行分析即可求解.
解答 解:(1)抛物线y=mx2+(3m-1)x-3,令y=0,
mx2+(3m-1)x-3=0,
${x}^{2}+(3-\frac{1}{m})x+3×(-\frac{1}{m})=0$,
解得x1=-3,x2=$\frac{1}{m}$,
由m为正整数,可知m=1,
所以抛物线的解析式为:y=x2+2x-3;
(2)y=x2+2x-3的顶点坐标为:(-1,-4),
由P(x1,k)与Q(x1+n,k)可知:直线PQ与x轴平行,
由翻折的性质可以得出:当-4≤k<-2,或k=0时,新图象与x轴恰好只有两个公共点.
点评 此题主要考查抛物线与x轴的交点问题,会运用一元二次方程的根解决抛物线与x轴交点问题,熟悉翻折性质并灵活运用解题是此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.下列四个命题中,真命题是( )
| A. | 对角线互相垂直平分的四边形是正方形 | |
| B. | 对角线相等且互相平分的四边形是矩形 | |
| C. | 对角线垂直相等的四边形是菱形 | |
| D. | 四边都相等的四边形是正方形 |
14.已知抛物线y=x2+bx+c的对称轴为x=1,若关于x的一元二次方程x2-bx-c=0在-3<x<2的范围内有解,则c的取值范围是( )
| A. | c≥-1 | B. | -1≤c<3 | C. | 3<c<8 | D. | -1≤c<8 |
11. 如图,这是某地2014年和2015年粮食作物产量的条形统计图,请你根据此图判断下列说法合理的是( )
如图,这是某地2014年和2015年粮食作物产量的条形统计图,请你根据此图判断下列说法合理的是( )
 如图,这是某地2014年和2015年粮食作物产量的条形统计图,请你根据此图判断下列说法合理的是( )
如图,这是某地2014年和2015年粮食作物产量的条形统计图,请你根据此图判断下列说法合理的是( )| A. | 2015年三类农作物的产量比2014年都有增加 | |
| B. | 玉米产量和杂粮产量增长率相当 | |
| C. | 2014年杂粮产量是玉米产量的约七分之一 | |
| D. | 2014年和2015年的小麦产量基本持平 |
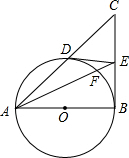 如图,在△ABC中,∠B=90°,以AB为直径的⊙O交AC于D,过点D作⊙O的切线交BC于E,AE交⊙O于点F.
如图,在△ABC中,∠B=90°,以AB为直径的⊙O交AC于D,过点D作⊙O的切线交BC于E,AE交⊙O于点F.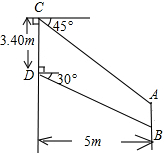 我国某型号飞机的机翼形状如图所示,AB∥CD,根据图中所给数据计算这块机翼的面积(结果精确到0.01m2,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
我国某型号飞机的机翼形状如图所示,AB∥CD,根据图中所给数据计算这块机翼的面积(结果精确到0.01m2,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)