题目内容
14.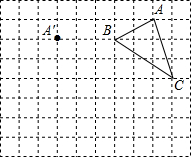 在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.(1)请画出平移后的△A′B′C′,并求△A′B′C′的面积;
(2)在图中找出格点D,使△ACD的面积与△ABC的面积相等.
分析 (1)根据图形平移的性质画出△A′B′C′,利用正方形的面积减去三个顶点上三角形的面积即可;
(2)过点B作直线l∥AC,直线l与格点的交点即为所求.
解答  解:(1)如图,△A′B′C′即为所求,
解:(1)如图,△A′B′C′即为所求,
S△A′B′C′=3×3-$\frac{1}{2}$×2×1-$\frac{1}{2}$×3×1-$\frac{1}{2}$×2×3=9-1-$\frac{3}{2}$-3=3.5;
(2)如图,点D1,D2即为所求.
点评 本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.

练习册系列答案
相关题目
16.某学校在开展“节约每一滴水”的活动中,从七年级的100名同学中任意选出20名同学汇报了各自家庭一个月的节水情况,将有关数据(每人上报节水量都是整整数)整理如下表:
请你估计这100名同学的家庭一个月节约用水的总量大约是230t.
| 节水量x/t | 0.5≤x<1.5 | 1.5≤x<2.5 | 2.5≤x<3.5 | 3.5≤x<4.5 |
| 人数 | 6 | 4 | 8 | 2 |
5.某商场欲购进果汁饮料和碳酸饮料共50箱,两种饮料每箱的进价和售价如表所示.设购进果汁饮料x箱(x为正整数),且所购进的两种饮料能全部卖出,获得的总利润为w元(注:总利润=总售价-总进价).
(1)求总利润w关于x的函数关系式;
(2)如果购进两种饮料的总费用不超过2100元,不低于1950元,那么该商场如何进货才能获利最多?并求出最大利润.
| 饮料 | 果汁饮料 | 碳酸饮料 |
| 进价(元/箱) | 51 | 36 |
| 售价(元/箱) | 61 | 43 |
(2)如果购进两种饮料的总费用不超过2100元,不低于1950元,那么该商场如何进货才能获利最多?并求出最大利润.
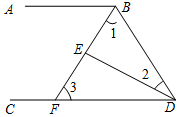 如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.
如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.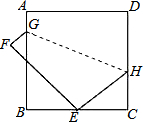 如图,正方形ABCD的边长为9,将正方形折叠,使D点落在BC边上的点E处,折痕为GH.若BE:EC=2:1,则线段CH的长是4.
如图,正方形ABCD的边长为9,将正方形折叠,使D点落在BC边上的点E处,折痕为GH.若BE:EC=2:1,则线段CH的长是4.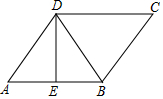 如图,在?ABCD中,D在AB的垂直平分线上,且?ABCD的周长为42cm,△BCD的周长比?ABCD的周长少12cm,则AB=12cm,S?ABCD=36$\sqrt{5}$cm2.
如图,在?ABCD中,D在AB的垂直平分线上,且?ABCD的周长为42cm,△BCD的周长比?ABCD的周长少12cm,则AB=12cm,S?ABCD=36$\sqrt{5}$cm2.