题目内容
9.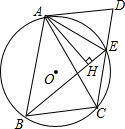 如图,已知四边形ABCD是平行四边形,AD与△ABC的外接圆⊙O恰好相切于点A,边CD与⊙O相交于点E,连接AE,BE.
如图,已知四边形ABCD是平行四边形,AD与△ABC的外接圆⊙O恰好相切于点A,边CD与⊙O相交于点E,连接AE,BE.(1)求证:AB=AC;
(2)若过点A作AH⊥BE于H,求证:BH=CE+EH.
分析 (1)根据弦切角定理和圆周角定理证明∠ABC=∠ACB,得到答案;
(2)作AF⊥CD于F,证明△AEH≌△AEF,得到EH=EF,根据△ABH≌△ACF,得到答案.
解答 证明:(1)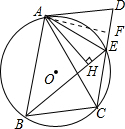 ∵AD与△ABC的外接圆⊙O恰好相切于点A,
∵AD与△ABC的外接圆⊙O恰好相切于点A,
∴∠ABE=∠DAE,又∠EAC=∠EBC,
∴∠DAC=∠ABC,
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠ABC=∠ACB,
∴AB=AC;
(2)作AF⊥CD于F,
∵四边形ABCE是圆内接四边形,
∴∠ABC=∠AEF,又∠ABC=∠ACB,
∴∠AEF=∠ACB,又∠AEB=∠ACB,
∴∠AEH=∠AEF,
在△AEH和△AEF中,
$\left\{\begin{array}{l}{∠AHE=∠AFE}\\{∠AEH=∠AEF}\\{AE=AE}\end{array}\right.$,
∴△AEH≌△AEF,
∴EH=EF,
∴CE+EH=CF,
在△ABH和△ACF中,
$\left\{\begin{array}{l}{∠ABH=∠ACF}\\{∠AHB=∠AFC}\\{AB=AC}\end{array}\right.$,
∴△ABH≌△ACF,
∴BH=CF=CE+EH.
点评 本题考查的是切线的性质和平行四边形的性质以及全等三角形的判定和性质,运用性质证明相关的三角形全等是解题的关键,注意圆周角定理和圆内接四边形的性质的运用.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
1.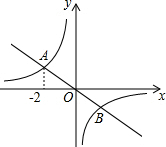 如图,双曲线y=$\frac{k}{x}$与直线y=-$\frac{1}{2}$x交于A、B两点,且A(-2,m),则点B的坐标是( )
如图,双曲线y=$\frac{k}{x}$与直线y=-$\frac{1}{2}$x交于A、B两点,且A(-2,m),则点B的坐标是( )
 如图,双曲线y=$\frac{k}{x}$与直线y=-$\frac{1}{2}$x交于A、B两点,且A(-2,m),则点B的坐标是( )
如图,双曲线y=$\frac{k}{x}$与直线y=-$\frac{1}{2}$x交于A、B两点,且A(-2,m),则点B的坐标是( )| A. | (2,-1) | B. | (1,-2) | C. | ($\frac{1}{2}$,-1) | D. | (-1,$\frac{1}{2}$) |

 如图,AB是⊙O的直径,$\widehat{ED}$=$\widehat{BD}$,连接ED、BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.
如图,AB是⊙O的直径,$\widehat{ED}$=$\widehat{BD}$,连接ED、BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C. 如图,△ABC≌△DEF,则EF=5.
如图,△ABC≌△DEF,则EF=5. 如图,是由四个完全相同的小正方形组成的立体图形,它的俯视图是( )
如图,是由四个完全相同的小正方形组成的立体图形,它的俯视图是( )