题目内容
(本题满分12分) 已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.



(1)如图①,若四边形ABCD是矩形,且DE⊥CF,求证 ;
;
(2)如图②,若四边形ABCD是平行四边形,试探究:当∠B与∠EGC满足什么关系时,使得 成立?并证明你的结论;
成立?并证明你的结论;
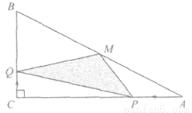
(3)如图③,若BA=BC=2,DA=DC= ,∠BAD=90°,DE⊥CF,试求
,∠BAD=90°,DE⊥CF,试求 的值.
的值.
(1)证明详见解析;(2)当∠B+∠EGC=180°时, 成立;理由详见解析;(3)
成立;理由详见解析;(3) .
.
【解析】
试题分析:(1)应用相似三角形的判定方法证得△ADE∽△DCF,应用相似三角形的性质得到比例式;
(2)在AD的延长线上取点M,使CM=CF,可以证得△ADE∽△DCM,得到比例式;
(3)过点C作CH⊥AD于H,可证△ADE∽△HCF,可以证得 .
.
试题解析:【解析】
(1)证明:∵四边形ABCD是矩形,∴∠A=∠ADC=90°,
∵DE⊥CF,∴∠ADE=∠DCF,∴△ADE∽△DCF,
∴ .
.
(2)当∠B+∠EGC=180°时, 成立.
成立.
证明如下: 在AD的延长线上取点M,使CM=CF,则∠CMF=∠CFM.

∵AB∥CD,∴∠A=∠CDM,
∵∠B+∠EGC=180°,
∴∠AED=∠FCB,∴∠CMF=∠AED.
∴△ADE∽△DCM,
∴ ,即
,即 .
.
(3)过点C作CH⊥AD于H,可证△ADE∽△HCF,
∴ .
.
考点:相似三角形的判定和性质.
考点分析: 考点1:图形的相似 形状相同,大小不同的两个图形相似 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目

 B.
B. C.
C. D.
D.
 B.
B. C.
C. D.
D.
 x2 - x +
x2 - x + .
.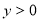 时,x的取值范围;
时,x的取值范围;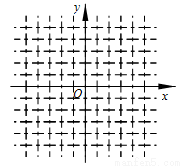
 △
△ 中,
中, ,
, 是
是 边上的中线,
边上的中线, ,则
,则 的值为 .
的值为 .
 +bx+c(a≠0)的图象如图所示,有下列结论:①
+bx+c(a≠0)的图象如图所示,有下列结论:① -4ac>0;②abc>0;③b=-2a ④9a+3b+c<0.其中,正确结论的个数是 ( )
-4ac>0;②abc>0;③b=-2a ④9a+3b+c<0.其中,正确结论的个数是 ( ) 