题目内容
(10分)某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
求销售单价为多少元时,每天的销售利润最大?最大利润是多少?
x=80元时有最大利润,最大利润为4500元.
【解析】
试题分析:根据总利润=单件利润×数量,单价利润=x-50,数量=50+5(100-x),然后根据二次函数的最值求法进行求解.
试题解析:y=(x-50)[50+5(100-x)]=(x-50)(-5x+550)=-5 +800x-27500
+800x-27500
∴y=-5 +800x-27500=-5
+800x-27500=-5 +4500
+4500
∵a=-5<0,∴抛物线开口向下.∵50≤x≤100,对称轴是直线x=80,
∴当x=80时,最大利润为4500元.
考点:二次函数的应用.
考点分析: 考点1:二次函数 定义:一般地,如果
 (a,b,c是常数,a≠0),那么y叫做x 的二次函数。
(a,b,c是常数,a≠0),那么y叫做x 的二次函数。 ①所谓二次函数就是说自变量最高次数是2;
②二次函数
 (a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时,
(a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时, 变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。
变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。③二次函数
 (a≠0)与一元二次方程
(a≠0)与一元二次方程 (a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:
(a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式: (1)一般式:
 (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0); (2)顶点式:
 (a,h,k是常数,a≠0)
(a,h,k是常数,a≠0) (3)当抛物线
 与x轴有交点时,即对应二次好方程
与x轴有交点时,即对应二次好方程 有实根x1和x2存在时,根据二次三项式的分解因式
有实根x1和x2存在时,根据二次三项式的分解因式 ,二次函数
,二次函数 可转化为两根式
可转化为两根式 。如果没有交点,则不能这样表示。
。如果没有交点,则不能这样表示。 二次函数的一般形式的结构特征:
①函数的关系式是整式;
②自变量的最高次数是2;
③二次项系数不等于零。 二次函数的判定:
二次函数的一般形式中等号右边是关于自变量x的二次三项式;
当b=0,c=0时,y=ax2是特殊的二次函数;
判断一个函数是不是二次函数,在关系式是整式的前提下,如果把关系式化简整理(去括号、合并同类项)后,能写成
 (a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
(a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 ,且与O相距6km的Q处.如图所示.货船的航行速度是____________km/h.(结果用根号表示.)
,且与O相距6km的Q处.如图所示.货船的航行速度是____________km/h.(结果用根号表示.)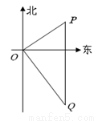



 ;
;  ,∠BAD=90°,DE⊥CF,试求
,∠BAD=90°,DE⊥CF,试求 的值.
的值. 是大气压中直径小于或等于
是大气压中直径小于或等于 的颗粒物,将
的颗粒物,将 用科学记数法表示为 .
用科学记数法表示为 .



 -3tan60°+
-3tan60°+ +
+ ;
; +k(a>0),其图象过点A(0,2),B(8,3),则h的值可以是( )
+k(a>0),其图象过点A(0,2),B(8,3),则h的值可以是( )
 的图象经过点
的图象经过点 ,则此反比例函数的图象在( )
,则此反比例函数的图象在( )