Question

已知AD是△ABC的中线，E是AD上一点，AE：ED=1：3，BE的延长线交AC于，求AF：FC．

Answer 1

考点：平行线分线段成比例,三角形中位线定理

专题：计算题

分析：作DG∥AC交BF于G，如图，根据平行线分线段成比例定理，由DG∥CF得

DG

CF

=

BD

BC

，即FC=2DG，由DG∥AF，

AF

DG

=

AE

ED

，则AF=

1

3

DG，然后计算AF：FC．

解答：解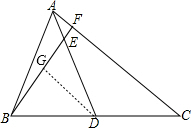：作DG∥AC交BF于G，如图，
∵AD是△ABC的中线，
∴BD=CD，
∵DG∥CF，
∴

DG

CF

=

BD

BC

=

1

2

，
∴FC=2DG，
∵DG∥AF，
∴

AF

DG

=

AE

ED

=

1

3

，
∴AF=

1

3

DG，
∴AF：FC=

1

3

DG：2DG=1：6．

点评：本题考查了平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例；平行于三角形的一边，并且和其他两边（或两边的延长线）相交的直线，所截得的三角形的三边与原三角形的三边对应成比例．也考查了比例的性质．