题目内容
已知在△ABC中,AB=5,AC=4,点D为AB上一点,且AD=2,E是AC边上的动点,当AE为何值时,△ADE与△ABC相似?
考点:相似三角形的判定
专题:
分析:题中没有指明具体的对应边,故应该分两种情况进行分析,分别是△ABC∽△ADE或△ABC∽△AED.
解答:解:∵△ABC与△ADE相似
∴△ABC∽△ADE或△ABC∽△AED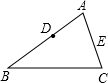 ,
,
①当△ABC∽△ADE时:
则AD:AB=AE:AC,即2:5=AE:4,
解得AE=
;
②当△ABC∽△AED时:
则AD:AC=AE:AB,即2:4=AE:5,
解得AE=
∴当AE=
或
时,△ABC与△ADE相似.
∴△ABC∽△ADE或△ABC∽△AED
 ,
,①当△ABC∽△ADE时:
则AD:AB=AE:AC,即2:5=AE:4,
解得AE=
| 8 |
| 5 |
②当△ABC∽△AED时:
则AD:AC=AE:AB,即2:4=AE:5,
解得AE=
| 5 |
| 2 |
∴当AE=
| 8 |
| 5 |
| 5 |
| 2 |
点评:此题考查了相似三角形的性质.此题难度适中,注意掌握分类讨论思想与数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知AB是⊙O的直径,CD是弦,AB⊥CD于点E,若AB=10,CD=6,则BE的长是( )
如图,已知AB是⊙O的直径,CD是弦,AB⊥CD于点E,若AB=10,CD=6,则BE的长是( )| A、4 | B、3 | C、2 | D、1 |
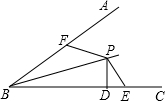 如图,已知BP平分∠ABC,PD⊥BC于D,BF+BE=2BD,求证:∠BFP+∠BEP=180°.
如图,已知BP平分∠ABC,PD⊥BC于D,BF+BE=2BD,求证:∠BFP+∠BEP=180°. 如图,∠A=∠D=90°,AB=DC,求证:AC=BD.
如图,∠A=∠D=90°,AB=DC,求证:AC=BD. 为了让广大青少年学生走向操场,走进自然,走到阳光下,积极参加体育锻炼.我国启动了“全国亿万学生阳光体育运动”.短跑运动,可以锻炼人的灵活性,增强人的爆发力,因此小明和小在课外活动中,报名参加了跑训练小组.在近几次百米训练中,所测成绩如图所示,请根据图中所示解答以下问题.分别计算他们的平均数、极差和方差填入下表格,若你是他们的教练,将小明与小亮的成绩比较后,你将分别给予他们怎样的建议?
为了让广大青少年学生走向操场,走进自然,走到阳光下,积极参加体育锻炼.我国启动了“全国亿万学生阳光体育运动”.短跑运动,可以锻炼人的灵活性,增强人的爆发力,因此小明和小在课外活动中,报名参加了跑训练小组.在近几次百米训练中,所测成绩如图所示,请根据图中所示解答以下问题.分别计算他们的平均数、极差和方差填入下表格,若你是他们的教练,将小明与小亮的成绩比较后,你将分别给予他们怎样的建议?