题目内容
14. 如图,⊙O是△ABC的外接圆,已知∠ABO=40°,则∠ACB的大小为( )
如图,⊙O是△ABC的外接圆,已知∠ABO=40°,则∠ACB的大小为( )| A. | 40° | B. | 30° | C. | 50° | D. | 60° |
分析 首先根据等腰三角形的性质及三角形内角和定理,求出∠AOB的度数,再利用圆周角与圆心角的关系,求出∠ACB的度数.
解答 解:△AOB中,OA=OB,∠ABO=40°;
∴∠AOB=180°-2∠ABO=100°;
∴∠ACB=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×100°=50°.
故选:C.
点评 本题主要考查了圆周角定理,等腰三角形的性质以及三角形内角和定理.在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6. 如图,已知AB=AC,AD=AE,∠BAC=∠DAE.下列结论不正确的是( )
如图,已知AB=AC,AD=AE,∠BAC=∠DAE.下列结论不正确的是( )
 如图,已知AB=AC,AD=AE,∠BAC=∠DAE.下列结论不正确的是( )
如图,已知AB=AC,AD=AE,∠BAC=∠DAE.下列结论不正确的是( )| A. | ∠BAD=∠CAE | B. | △ABD≌△ACE | C. | AB=BC | D. | BD=CE |
 如图是一个台阶的示意图,台阶横长5m,如果要在台阶上铺地毯,那么至少要买地毯多少平方米?
如图是一个台阶的示意图,台阶横长5m,如果要在台阶上铺地毯,那么至少要买地毯多少平方米?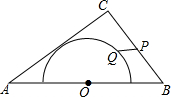 如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P、Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是9.
如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P、Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是9. 如图,在⊙O内接四边形ABCD中,∠ABC=60°,AB=BC=6,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为11$\sqrt{3}$,则△BEF的面积为5$\sqrt{3}$.
如图,在⊙O内接四边形ABCD中,∠ABC=60°,AB=BC=6,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为11$\sqrt{3}$,则△BEF的面积为5$\sqrt{3}$.