题目内容
14. 如图,在菱形ABCD中,E为边CD上一点,连结AE并延长,交BC的延长线于点F,若CE=1,DE=2,则CF长为( )
如图,在菱形ABCD中,E为边CD上一点,连结AE并延长,交BC的延长线于点F,若CE=1,DE=2,则CF长为( )| A. | 1 | B. | 1.5 | C. | 2 | D. | 2.5 |
分析 根据菱形的性质得到AD=CD=CE+DE=3,AD∥BC,推出△ADE∽△CFE,根据相似三角形的性质得到$\frac{AD}{CF}=\frac{DE}{CE}$,代入数据即可得到结论.
解答 解:在菱形ABCD中,
∵AD=CD=CE+DE=3,AD∥BC,
∴△ADE∽△CFE,
∴$\frac{AD}{CF}=\frac{DE}{CE}$,
∴$\frac{3}{CF}=\frac{2}{1}$,
∴CF=1.5,
故选B.
点评 此题考查了相似三角形的判定和性质,菱形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
19.下列方程中,是一元一次方程的是( )
| A. | x2-4x=3 | B. | $\frac{y}{2}$+2y=3 | C. | x+2y=1 | D. | x-1=$\frac{1}{x}$ |
6.下列方程是一元一次方程的是( )
| A. | x2-x=2 | B. | x+5y=3 | C. | $\frac{1}{x}$+1=$\frac{x}{2}$ | D. | $\frac{1}{2}$+x=$\frac{x}{5}$ |
4.将下列多项式分解因式,结果中不含因式x+1的是( )
| A. | x2-1 | B. | x2-2x+1 | C. | x(x-2)+(x-2) | D. | x2+2x+1 |
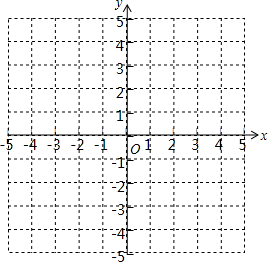 如图,描出A(-3,-2)、B(2,-2)、C(3,1)、D(-2,1)四个点,顺次连接A、B、C、D四点,求四边形ABCD的面积.
如图,描出A(-3,-2)、B(2,-2)、C(3,1)、D(-2,1)四个点,顺次连接A、B、C、D四点,求四边形ABCD的面积.