题目内容
在面积为24的△ABC中,矩形DEFG的边DE在AB上运动,点F、G分别在BC、AC上.
(1)若AE=8,DE=2EF,求GF的长;
(2)若∠ACB=90°,如图2,线段DM、EN分别为△ADG和△BEF的角平分线,求证:MG=NF.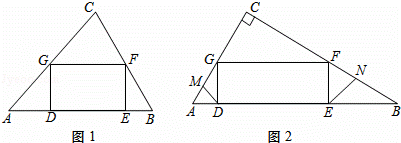
(1)解:作CH⊥AB于H,交GF于K,如图1,
∵S△ABC= ×AB×CH=24,AB=8,
×AB×CH=24,AB=8,
∴CH=6,
设EF=x,则KH=x,GF=DE=2x,CK=6﹣x,
∵GF∥AB,
∴△CGF∽△CAB.
∴ =
= ,即
,即 =
=
∴x=2.4,
∴GF=4.8;
(2)证明:过点G、D分别作GP∥BC,DP∥EN,它们相交于点P,在DM上截取DQ=DP,连接QG,如图2,
在△GPD和△FNE中

∴△GPD≌△FNE,
∴FN=GP,
∵线段DM、EN分别为△ADG和△BEF的角平分线,
∴∠MDG=∠FEN=∠GDP=45°,
在△GDQ和△GDP中
 ,
,
∴△GPD≌△GQD,
∴GQ=GP,∠GQD=∠GPD,
∵GP∥BC,
∴∠MGP=∠C=90°,
而∠MDP=45°+45°=90°,
∴∠GMD+∠GPD=180°,
而∠GMD+∠GMQ=180°,
∴∠GMQ=∠GQM,
∴GM=GQ,
∴MG=NF.


练习册系列答案
相关题目
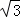 ,山坡坡面上点 E处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.
,山坡坡面上点 E处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.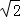 ≈1.414,
≈1.414,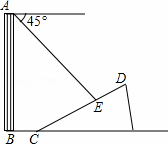
 和
和 ,则袋中黄球有
,则袋中黄球有  图象上的概率.
图象上的概率. B.
B.  C.
C.  D.
D. 

 中自变量x的取值范围是( )
中自变量x的取值范围是( )