��Ŀ����
��ͼ����ƽ��ֱ������ϵ�У���ֱ֪��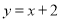 ��
��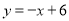 ��
��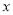 ��ֱ��ཻ�ڵ�
��ֱ��ཻ�ڵ�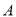 �͵�
�͵�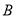 ������ֱ���ཻ�ڵ�
������ֱ���ཻ�ڵ�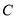 ����
����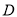 Ϊ
Ϊ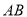 ���е㣬��
���е㣬��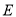 ���߶�
���߶�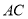 ��һ�����㣨�����
��һ�����㣨�����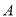 ��
��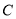 �غϣ�������
�غϣ�������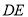 ��������
��������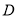 ��
��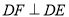 ��
��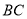 �ڵ�
�ڵ�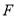 ��
��
��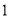 ���ж�
���ж�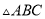 ����״����˵�����ɣ�
����״����˵�����ɣ�
��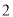 ������
������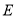 ���߶�
���߶�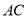 ���˶�ʱ���ı���
���˶�ʱ���ı���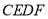 ������Ƿ�Ϊ��ֵ�����ǣ�����������ֵ�������ǣ���˵�����ɣ�
������Ƿ�Ϊ��ֵ�����ǣ�����������ֵ�������ǣ���˵�����ɣ�
��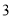 ������
������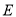 �ĺ�����Ϊ
�ĺ�����Ϊ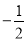 ʱ����
ʱ����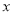 �����ҵ�һ��
�����ҵ�һ��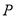 ʹ��
ʹ��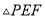 ���ܳ���С����ֱ��д����
���ܳ���С����ֱ��д����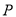 �����꣮
�����꣮
��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ


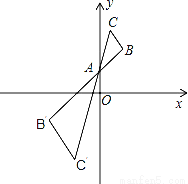
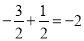 B.
B. 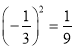 C.
C. 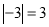 D.
D. 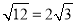
 �ij���������
�ij���������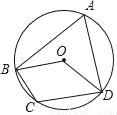
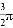 C. 2�� D. 3��
C. 2�� D. 3��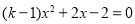 ����������ȵ�ʵ��������k��ȡֵ��Χ�� ��
����������ȵ�ʵ��������k��ȡֵ��Χ�� �� ����д���ò���ʽ��������⣮
����д���ò���ʽ��������⣮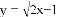 �У��Ա���
�У��Ա���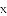
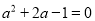 �������ʽ
�������ʽ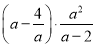 ��ֵ.
��ֵ.