题目内容
11.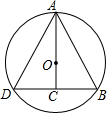 如图,Rt△ABC中,∠C=90°、∠BAC=30°,在AC边上取点O画圆使⊙O经过A、B两点,延长BC交⊙O于D;求证:A、B、D是⊙O的三等分点.
如图,Rt△ABC中,∠C=90°、∠BAC=30°,在AC边上取点O画圆使⊙O经过A、B两点,延长BC交⊙O于D;求证:A、B、D是⊙O的三等分点.
分析 根据垂径定理求出DC=BC,由线段垂直平分线的性质得出AD=AB,证出△ADB是等边三角形,由圆心角、弧、弦的关系得出$\widehat{AD}=\widehat{AB}=\widehat{BD}$即可.
解答 证明:∵∠ACB=90°,
即AC⊥BD,
∴DC=BC,
∴AD=AB,
∵∠BAC=30°,
∴∠ABC=60°,
∴△ADB是等边三角形,
∴AD=AB=BD,
∴$\widehat{AD}=\widehat{AB}=\widehat{BD}$,
即A、B、D是⊙O的三等分点.
点评 本题考查了垂径定理,圆心角、弧、弦之间的关系,直角三角形的性质,等边三角形的判定与性质;熟练掌握圆心角、弧、弦的关系定理,证明三角形是等边三角形是解决问题的关键.

练习册系列答案
相关题目
2.“9的算术平方根”记作$\sqrt{9}$,其值是( )
| A. | 3 | B. | -3 | C. | ±3 | D. | 9 |
6.对函数y=-x2-2x-3的最大(小)值判断正确的是( )
| A. | 有最大值-1 | B. | 有最小值-1 | C. | 有最大值-2 | D. | 有最小值-2 |
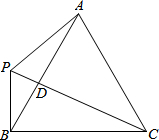 如图,△ABC为等边三角形,P是直线AB左侧一点,连接PA、PB、PC,PC与AB相交于点D,∠BPC=60°.
如图,△ABC为等边三角形,P是直线AB左侧一点,连接PA、PB、PC,PC与AB相交于点D,∠BPC=60°.



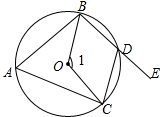 如图所示,已知四边形ABDC是圆内接四边形,∠1=112°,则∠CDE=56度.
如图所示,已知四边形ABDC是圆内接四边形,∠1=112°,则∠CDE=56度.