题目内容
如图，把一根圆柱形的木头锯成正方体形的柱子，使截面正方形的四个顶点均在圆上．（1）正方形的对角线与圆的直径有什么关系？
（2）设圆O的半径为2，求圆中阴影部分的面积之和．
考点：正多边形和圆
专题：
分析：（1）直接根据圆周角定理即可得出结论；
（2）先根据勾股定理求出AD的长，再根据S阴影=S⊙O-S正方形ABCD即可得出结论．
（2）先根据勾股定理求出AD的长，再根据S阴影=S⊙O-S正方形ABCD即可得出结论．
解答：
解：（1）连接AC，
∵∠D=90°，点D在⊙O上，
∴正方形的对角线是圆的直径；
（2）∵四边形ABCD是正方形，
∴AD=CD．
∵圆O的半径为2，
∴2AD2=AC2，即2AD2=42，解得AD=2
，
∴S阴影=S⊙O-S正方形ABCD=π×22-（2
）2=4π-8．
解：（1）连接AC，∵∠D=90°，点D在⊙O上，
∴正方形的对角线是圆的直径；
（2）∵四边形ABCD是正方形，
∴AD=CD．
∵圆O的半径为2，
∴2AD2=AC2，即2AD2=42，解得AD=2
| 2 |
∴S阴影=S⊙O-S正方形ABCD=π×22-（2
| 2 |
点评：本题考查的是正多边形和圆，熟知正方形的性质是解答此题的关键．
练习册系列答案
相关题目
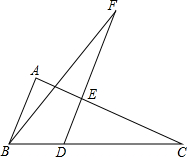如图，△ABC的面积为63，D是BC上的一点，且BD：CD=1：2，DE∥AB交AC于点E，延长DE到F，使FE：ED=2：1，连接BF，则△BDF的面积为 （ ）
如图，抛物线y=-x2+2（m+1）x+m+3与x轴交于A，B两点，且OA：OB=1：3，求m的值．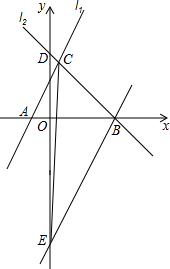
如图，直线l1，l2，交于C点，直线l1与x轴交于A，直线l2与x轴交于B（3，0），与y轴交于D（0，3），已知直线l1的函数解析式为y=2x+2．
如图，在四边形ABCD中，AB∥CD，对角线AC、BD相交于点O，若△COD的面积为a2，△AOB的面积为b2，其中a＞0，b＞0．求△AOD的面积．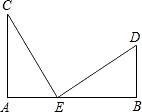
已知，如图，AC⊥AB，DB⊥AB，AC=BE，AE=BD，