题目内容
 如图,某地方政府决定在相距50km的A、B两站之间的公路旁E点,修建一个土特产加工基地,且使C、D两村到E点的距离相等,已知DA⊥AB于A,CB⊥AB于B,DA=30km,CB=20km,那么基地E应建在离A站多少千米的地方?
如图,某地方政府决定在相距50km的A、B两站之间的公路旁E点,修建一个土特产加工基地,且使C、D两村到E点的距离相等,已知DA⊥AB于A,CB⊥AB于B,DA=30km,CB=20km,那么基地E应建在离A站多少千米的地方?考点:勾股定理的应用
专题:
分析:由勾股定理两直角边的平方和等于斜边的平方即可求,即在直角三角形DAE和直角三角形CBE中利用斜边相等两次利用勾股定理得到AD2+AE2=BE2+BC2,设AE为x,则BE=10-x,将DA=8,CB=2代入关系式即可求得.
解答:解:设基地E应建在离A站x千米的地方.
则BE=(50-x)千米
在Rt△ADE中,根据勾股定理得:AD2+AE2=DE2
∴302+x2=DE2…(3分)
在Rt△CBE中,根据勾股定理得:CB2+BE2=CE2
∴202+(50-x)2=CE2
又∵C、D两村到E点的距离相等.
∴DE=CE∴DE2=CE2
∴302+x2=202+(50-x)2
解得x=20
∴基地E应建在离A站多少20千米的地方.
则BE=(50-x)千米
在Rt△ADE中,根据勾股定理得:AD2+AE2=DE2
∴302+x2=DE2…(3分)
在Rt△CBE中,根据勾股定理得:CB2+BE2=CE2
∴202+(50-x)2=CE2
又∵C、D两村到E点的距离相等.
∴DE=CE∴DE2=CE2
∴302+x2=202+(50-x)2
解得x=20
∴基地E应建在离A站多少20千米的地方.
点评:考查了勾股定理的应用,本题主要是运用勾股定理将两个直角三角形的斜边表示出来,两边相等求解即可.

练习册系列答案
相关题目
 如图,∠1的同位角是
如图,∠1的同位角是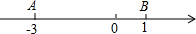 已知:如图数轴上两动点A、B原始位置所对应的数分别为-3、1,
已知:如图数轴上两动点A、B原始位置所对应的数分别为-3、1,