题目内容
18. 如图,在△ABC中,D、E分别是AC、AB上的中点,且BD≠CE,求证:AB≠AC.
如图,在△ABC中,D、E分别是AC、AB上的中点,且BD≠CE,求证:AB≠AC.
分析 设AB=AC即可证明△BCD≌△CBE,从而证明BE=CE,与已知相矛盾,据此即可证得.
解答 证明:设AB=AC,则∠ABC=∠ACB,
∵AB=AC,D、E分别是AC、AB上的中点,
∴BE=CD,
在△BCD和△CBE中,$\left\{\begin{array}{l}{BE=CD}\\{∠ABC=∠ACB}\\{BC=CB}\end{array}\right.$,
∴△BCD≌△CBE,
∴BD=CE,与BD≠CE相矛盾.
则AB≠AC.
点评 本题结合角的比较考查反证法,解此题关键要懂得反证法的意义及步骤.
反证法的步骤是:
(1)假设结论不成立;
(2)从假设出发推出矛盾;
(3)假设不成立,则结论成立.
在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
15.农科所为了考察某种水稻穗长的分布情况,在一块试验田里随机抽取了52个谷穗作为样本,量得它们的长度(单位:cm).对样本数据适当分组后,列出了如下频数分布表:
(1)请你在图1,图2中分别绘出频数分布直方图和频数折线图;
(2)请你对这块试验田里的水稻穗长进行分析;
(3)求这块试验田里穗长在5.5≤x<7范围内的谷穗的概率.
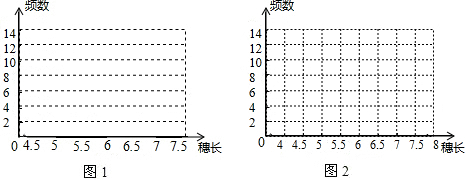
| 穗长 | 4.5≤x<5 | 5≤x<5.5 | 5.5≤x<6 | 6≤x<6.5 | 6.5≤x<7 | 7≤x<7.5 |
| 频数 | 4 | 8 | 12 | 13 | 10 | 5 |
(2)请你对这块试验田里的水稻穗长进行分析;
(3)求这块试验田里穗长在5.5≤x<7范围内的谷穗的概率.


 如图,已知△AOB、△COD都是等腰直角三角形,∠AOB=∠COD=90°,N、M、Q、P分别为AB、CB、CD、AD的中点.求证:四边形NMQP为正方形.
如图,已知△AOB、△COD都是等腰直角三角形,∠AOB=∠COD=90°,N、M、Q、P分别为AB、CB、CD、AD的中点.求证:四边形NMQP为正方形.