题目内容
9.(1)解分式方程:x-$\frac{2}{x+1}=\frac{2x}{x+1}$;(2)解不等式组并把它的解集在数轴上表示出来:$\left\{\begin{array}{l}{3x+1≤4}\\{3-\frac{1}{2}x<4}\end{array}\right.$.
分析 (1)观察可得最简公分母是x+1,方程两边乘最简公分母,可以把分式方程转化为整式方程求解;
(2)根据一元一次不等式组的解法求出不等式组的解集,再在数轴上表示出来即可.
解答 解:(1)方程两边同乘x+1,
得:x(x+1)-2=2x,
整理得:x2-x-2=0
解得:x1=2,x2=-1.
经检验:当x=2时,x+1≠0,
当x=-1时,x+1=0,
∴x=2是原方程的解.
(2)$\left\{\begin{array}{l}{3x+1≤4}\\{3-\frac{1}{2}x<4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x≤1}\\{x>-2}\end{array}\right.$,
∴不等式组的解集:-2<x≤1,
点评 本题考查了分式方程和解不等式组,解决本题的关键是把分式方程转化为整式方程解析解答.

练习册系列答案
相关题目
20.若分式$\frac{3}{x-2}$有意义,则x应满足的条件是( )
| A. | x≠0 | B. | x≥2 | C. | x≠2 | D. | x≤2 |
17.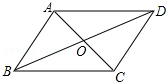 如图,四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是( )
如图,四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是( )
 如图,四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是( )
如图,四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是( )| A. | AB=DC,AD=BC | B. | AB∥DC,AO=BO | C. | AB=DC,∠B=∠D | D. | AB∥DC,∠B=∠D |
1.若x>y,则下列式子错误的是( )
| A. | x-3>y-3 | B. | -x>-y | C. | x+3>y+2 | D. | $\frac{x}{3}$>$\frac{y}{3}$ |
18. 如图所示,∠BAC和∠ACD是( )
如图所示,∠BAC和∠ACD是( )
 如图所示,∠BAC和∠ACD是( )
如图所示,∠BAC和∠ACD是( )| A. | 同位角 | B. | 同旁内角 | C. | 内错角 | D. | 以上结论都不对 |
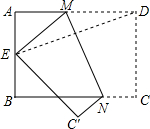 如图,四边形ABCD为矩形,AB=6,BC=8,E为AB的中点,将矩形ABCD折叠,使得点D与点E重合,折痕为MN,则折痕MN的长度为$\frac{3\sqrt{73}}{4}$.
如图,四边形ABCD为矩形,AB=6,BC=8,E为AB的中点,将矩形ABCD折叠,使得点D与点E重合,折痕为MN,则折痕MN的长度为$\frac{3\sqrt{73}}{4}$.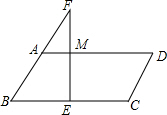 如图,在?ABCD中,边BC的垂直平分线EF分别交AD、BC于点M、E,交BA的延长线于点F.若点A是BF的中点,AB=5,?ABCD的周长为34,则FM的长为( )
如图,在?ABCD中,边BC的垂直平分线EF分别交AD、BC于点M、E,交BA的延长线于点F.若点A是BF的中点,AB=5,?ABCD的周长为34,则FM的长为( )