题目内容
7.如图,在四边形ABCD中,∠ABC=∠ADC=90°,AB=BC=10,AD=2DC,连对角线AC、BD相交于点E(1)①求证:BD平分∠ADC;②计算$\frac{AE}{CE}$的值
(2)如图2,点P是DE上一动点,连PC,过点P作PQ⊥PC交边AB于点Q,过点Q作QF⊥BD于点F,当P点运动过程中,猜想PF与BD的数量关系并证明.
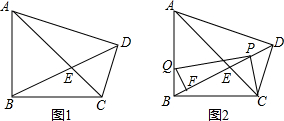
分析 (1)如图1,①解法一,根据对角互补的四边形四点共圆得:A、B、C、D四点共圆,由同弧所对的圆周角相等得:∠BAC=∠BDC,∠ACB=∠ADB,由等腰直角△ABC可知:∠BAC=∠ACB=45°,所以∠BDC=∠ADB=45°,从而得结论;
解法二,取两直角三角形斜边AC的中点G,根据直角三角形斜边中线等于斜边的一半构建两个等腰三角形,利用等腰三角形三线合一得:BG⊥AC,则∠AGB=90°,再根据等边对等角和外角定理可得出结论;
②由角平分线性质列比例式得出;
(2)如图2,BD=$\frac{3}{2}$FP,理由是:先根据勾股定理求AC、AD、DC的长,由$\frac{AE}{EC}$=2求EC的长,过C作CM⊥BD于M,构建直角△CMP,证明△QFP∽△PMC,列比例式$\frac{FQ}{PM}=\frac{FP}{MC}$,设BF=a,则QF=2a,代入列方程求出PM=a,得到FP=2MC,再由线段的和得出结论.
解答 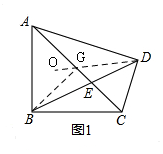 证明:(1)如图1,①解法一:∵∠ABC=∠ADC=90°,
证明:(1)如图1,①解法一:∵∠ABC=∠ADC=90°,
∴A、B、C、D四点共圆,
∴∠BAC=∠BDC,∠ACB=∠ADB,
∵AB=BC,∠ABC=90°,
∴∠BAC=∠ACB=45°,
∴∠BDC=∠ADB=45°,
∴BD平分∠ADC;
解法二:取AC的中点G,连接BG,做射线DG,
∵∠ABC=∠ADC=90°,
∴BG=$\frac{1}{2}$AC,DG=$\frac{1}{2}$AC,
∴AG=DG=BG,
∴∠GAD=∠ADG,∠GBD=∠GDB,
设∠ADG=x,∠GDB=y,
∴∠ADB=x+y,
∵AB=BC,G是AC的中点,
∴BG⊥AC,
∴∠AGB=90°,
∵∠AGO=∠GAD+∠ADG=2x,∠BGO=∠GBD+∠GDB=2y,
∴2x+2y=90°,
x+y=45°,
∴∠ADB=45°,
∴∠ADB=∠BDC=45°,
∴BD平分∠ADC;
②∵BD平分∠ADC;
∴$\frac{AD}{DC}=\frac{AE}{CE}$,
∵AD=2DC,
∴$\frac{AE}{CE}$=2;
(2)如图2,BD=$\frac{3}{2}$FP,理由是:
在Rt△ABC中,AB=BC=10,
∴AC=$\sqrt{1{0}^{2}+1{0}^{2}}$=10$\sqrt{2}$,
由$\frac{AE}{EC}$=2得:EC=$\frac{1}{3}$AC=$\frac{10\sqrt{2}}{3}$,
在Rt△ADC中,设DC=x,则AD=2x,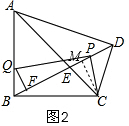
则x2+(2x)2=(10$\sqrt{2}$)2,
解得:x=±2$\sqrt{10}$,
∴CD=2$\sqrt{10}$,AD=4$\sqrt{10}$,
过C作CM⊥BD于M,
∵∠BDC=45°,
∴△MDC为等腰直角三角形,
∴CM=DM=$\frac{CD}{\sqrt{2}}$=$\frac{2\sqrt{10}}{\sqrt{2}}$=2$\sqrt{5}$,
由勾股定理得:BM=$\sqrt{B{C}^{2}-C{M}^{2}}$=$\sqrt{1{0}^{2}-(2\sqrt{5})^{2}}$=4$\sqrt{5}$,
∵∠DBC+∠ABD=90°,
∠ABD+∠BQF=90°,
∴∠DBC=∠BQF,
∵∠DBC=∠CAD,
∴∠BQF=∠CAD,
∵tan∠CAD=$\frac{CD}{AD}$=$\frac{1}{2}$,
∴tan∠BQF=$\frac{BF}{QF}$=$\frac{1}{2}$,
设BF=a,则QF=2a,
同理得∠MPC=∠FQP,
∵∠CMP=∠QFP=90°,
∴△QFP∽△PMC,
∴$\frac{FQ}{PM}=\frac{FP}{MC}$,
∴$\frac{2a}{PM}=\frac{PM+4\sqrt{5}-a}{2\sqrt{5}}$,
(PM+4$\sqrt{5}$)(PM-a)=0,
∴PM=a,
∴$\frac{FP}{MC}=\frac{2}{1}=2$,
∴FP=2MC=2MD=2(MP+PD)=2(BF+PD),
∴BD=BF+PD+FP=$\frac{1}{2}$FP+FP=$\frac{3}{2}$FP.
点评 本题是四边形的综合题,考查了四点共圆的判定和性质、等腰直角三角形、角平分线等性质,四边形与三角形结合,相似与三角函数相结合,列比例式,并设未知数,代入列方程可求解.

 科学实验活动册系列答案
科学实验活动册系列答案| 每箱售价x(元) | 68 | 67 | 66 | 65 | … | 40 |
| 每天销量y(箱) | 40 | 45 | 50 | 55 | … | 180 |
(1)求y与x的函数解析式;
(2)水蜜桃的进价是40元/箱,若该超市每天销售水蜜桃盈利1600元,要使顾客获得实惠,每箱售价是多少元?
(3)七月份连续阴雨,销售量减少,超市决定采取降价销售,所以从7月17号开始水蜜桃销售价格在(2)的条件下,下降了m%,同时水蜜桃的进货成本下降了10%,销售量也因此比原来每天获得1600元盈利时上涨了2m%(m<100),7月份(按31天计算)降价销售后的水蜜桃销售总盈利比7月份降价销售前的销售总盈利少7120元,求m的值.
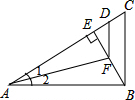 如图:AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则( )
如图:AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则( )| A. | ∠1=∠EFD | B. | BE=EC | C. | BF=CD | D. | FD∥BC |
