题目内容
一件工作,甲做3小时,乙做8个小时,能完成这件工作的
,甲乙合作了3小时,再由乙独做1小时,能完成这件工作的
,求这件工作由甲、乙单独完成,各需几小时.
| 13 |
| 30 |
| 3 |
| 10 |
考点:二元一次方程组的应用
专题:
分析:把工作总量看作“1”.设甲单独完成该工作需要x小时,乙单独完成该工作需要y小时.由“工作效率=工作量÷工作时间”求得甲、乙的工作效率.依据“甲做3小时,乙做8个小时,能完成这件工作的
”、“甲乙合作了3小时,再由乙独做1小时,能完成这件工作的
”列出方程组,通过解方程组求得x、y的值.
| 13 |
| 30 |
| 3 |
| 10 |
解答:解:设甲单独完成该工作需要x小时,乙单独完成该工作需要y小时.则
,
解得
.
答:这件工作由甲、乙单独完成,分别需要18小时、30小时.
|
解得
|
答:这件工作由甲、乙单独完成,分别需要18小时、30小时.
点评:本题考查了二元一次方程组的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.利用二元一次方程组求解的应用题一般情况下题中要给出2个等量关系,准确的找到等量关系并用方程组表示出来是解题的关键.

练习册系列答案
相关题目
 如图,点E、F分别在平行四边形ABCD的边DC和AB上,且DF∥BE,EF交BD于点O,那么四边形FBED是平行四边形吗?
如图,点E、F分别在平行四边形ABCD的边DC和AB上,且DF∥BE,EF交BD于点O,那么四边形FBED是平行四边形吗?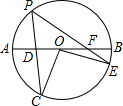 如图所示,AB是⊙O的直径,弦PC交OA于点D,弦PE交OB于点F,且OC=DC,OF=EF,若∠C=∠PFA,则∠CPE=
如图所示,AB是⊙O的直径,弦PC交OA于点D,弦PE交OB于点F,且OC=DC,OF=EF,若∠C=∠PFA,则∠CPE=