题目内容
6.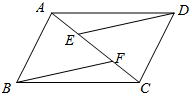 如图,?ABCD中,E、F为AC上的两点,AE=CF,求证:DE=BF.
如图,?ABCD中,E、F为AC上的两点,AE=CF,求证:DE=BF.
分析 根据平行四边形的性质可得AD=BC,AD∥BC,利用平行线的性质可得∠DAE=∠BCF,然后利用SAS判定△ADE≌△CBF,从而可得DE=BF.
解答 证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAE=∠BCF,
在△ADE和△CBF中$\left\{\begin{array}{l}{AE=CF}\\{∠DAE=∠BCF}\\{AD=CB}\end{array}\right.$,
∴△ADE≌△CBF(SAS)
∴DE=BF.
点评 此题主要考查了平行四边形的性质,以及全等三角形的判定和性质,关键是掌握平行四边形对边平行且相等.

练习册系列答案
相关题目
16.已知点A的坐标为(2,3),O为坐标原点,连接OA,将线段OA绕点A按顺时针方向旋转90°得AB,则点B的坐标为( )
| A. | (5,1) | B. | (-3,2) | C. | (-1,5) | D. | (3,-2) |
18.下列各式中,无意义的是( )
| A. | -$\sqrt{-3}$ | B. | -$\sqrt{|-3|}$ | C. | -$\sqrt{-(-3)}$ | D. | $\root{3}{-3}$ |
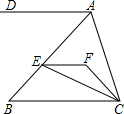 如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=100°,∠ACF=20°,求∠FEC的度数.
如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=100°,∠ACF=20°,求∠FEC的度数.