题目内容
4.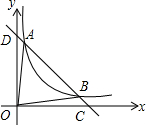 如图,直线y=-x向上平移m个单位长度得到直线l,已知直线l与双曲线y=$\frac{k}{x}$(x>0)交于A,B两点,与x轴,y轴交于点C,点D,其中点A坐标为(1,6)
如图,直线y=-x向上平移m个单位长度得到直线l,已知直线l与双曲线y=$\frac{k}{x}$(x>0)交于A,B两点,与x轴,y轴交于点C,点D,其中点A坐标为(1,6)(1)m=7,k=6,点B坐标为(6,1);
(2)连接OA,OB,求△OAB的面积;
(3)请在y轴上确定一点P,使PA+PB的值最小.
分析 (1)直线AB的解析式是y=-x+m,把(1,6)代入即可求得m的值,利用待定系数法即可求得k的值,根据对称性即可求得B的坐标;
(2)根据S△OAB=S△OCD-S△ODA-S△OCB即可求解;
(3)求得A关于y轴的对称点,求出经过这点和B的直线的解析式,然后求得直线和y轴的交点即可.
解答 解:(1)直线AB的解析式是y=-x+m,把(1,6)代入得-1+m=6,
解得:m=7.
把(1,6)代入y=$\frac{k}{x}$得k=6.
∵y=$\frac{6}{x}$和直线y=-x+7都关于一、三象限的角平分线对称,
∴B的坐标是(6,1).
故答案是:7,6,(6,1);
(2)在y=-x+7中,令x=0,解得y=7,
令y=0,解得x=7,则C的坐标是(7,0),D的坐标是(0,7).
则S△OAB=S△OCD-S△ODA-S△OCB=$\frac{1}{2}$×7×7-$\frac{1}{2}$×1×7-$\frac{1}{2}$×1×7=$\frac{35}{2}$;
(3)A关于y轴的对称点是(-1,6),设经过这点和B的直线的解析式是y=mx+n,
根据题意得:$\left\{\begin{array}{l}{-m+n=6}\\{6m+n=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=-\frac{5}{7}}\\{n=\frac{37}{7}}\end{array}\right.$.
则直线的解析式是y=-$\frac{5}{7}$x+$\frac{37}{7}$,令x=0,解得y=$\frac{37}{7}$,
则P的坐标是(0,$\frac{37}{7}$).
点评 本题考查了待定系数求函数的解析式以及反比例函数的轴对称性,正确求得B的坐标是关键.

| 通话时间x/min | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 |
| 频数(通话次数) | 20 | 16 | 9 | 5 |
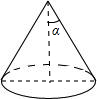 如图,圆锥的底面半径为3,侧面积为18π,设圆锥的母线与高的夹角为α,则tanα的值是( )
如图,圆锥的底面半径为3,侧面积为18π,设圆锥的母线与高的夹角为α,则tanα的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | 2 |
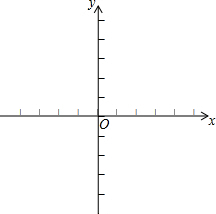 如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于A(-3,0)、B(1,0)两点,与y轴交于点C,D是抛物线的顶点,E是对称轴与x轴的交点.
如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于A(-3,0)、B(1,0)两点,与y轴交于点C,D是抛物线的顶点,E是对称轴与x轴的交点.