题目内容
3.已知a,b表示两个实数,定义运算:“△”、“○”,a△b=a(a+b),a○b=a-b-3,则关于x的表达式x2○[(x-2)△3]≥0的解集是( )| A. | x≥1 | B. | x≤1 | C. | x≤-5 | D. | x≥-1 |
分析 根据题目中的新定义可以对所求的不等式进行逐步化简,最终可以求得不等式的解集.
解答 解:∵a△b=a(a+b),a○b=a-b-3,
∴x2○[(x-2)△3]≥0,
∴x2○[(x-2)(x-2+3)]≥0,
化简,得
x2○(x2-x-2)≥0,
∴x2-(x2-x-2)-3≥0,
化简,得
x-1≥0,
解得x≥1,
故选A.
点评 本题考查整式的运算、解一元一次不等式,新定义,解题的关键是明确新定义,会运用新定义对所求的式子进行化简,注意计算过程中一定要仔细认真.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
11.设2m=8,2n=32,则2m+3n等于( )
| A. | 12 | B. | 21 | C. | 45 | D. | 64 |
12.下列等式正确的是( )
| A. | $\sqrt{16}=±4$ | B. | $\sqrt{-16}=-4$ | C. | $\root{3}{-8}=-\root{3}{8}$ | D. | $±\sqrt{16}=4$ |
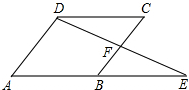 已知:如图,在?ABCD中,延长AB到点E,使BE=AB,连接DE交BC于点F.求证:△BEF≌△CDF.
已知:如图,在?ABCD中,延长AB到点E,使BE=AB,连接DE交BC于点F.求证:△BEF≌△CDF.
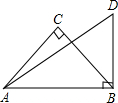 已知:如图,∠ABD=∠C=90°,AD=12,BD=6,AC=BC.
已知:如图,∠ABD=∠C=90°,AD=12,BD=6,AC=BC.