题目内容
 如图,三角板ABC中,∠ACB=90°,AB=2,∠A=30°,三角板ABC绕直角顶点C顺时针旋转90°得到△A1B1C,求:
如图,三角板ABC中,∠ACB=90°,AB=2,∠A=30°,三角板ABC绕直角顶点C顺时针旋转90°得到△A1B1C,求:(1)弧AA1的长;
(2)在这个旋转过程中三角板AC边所扫过的扇形ACA1的面积;
(3)在这个旋转过程中三角板所扫过的图形面积;
(4)在这个旋转过程中三角板AB边所扫过的图形面积.
分析:(1)根据直角三角形30°角所对的直角边等于斜边的一半求出BC,再根据勾股定理列式求出AC的长,然后利用弧长公式列式计算即可得解;
(2)根据扇形的面积公式列式计算即可得解;
(3)设弧BB1与AB相交于D,可得△BCD是等边三角形,根据等边三角形的性质求出BD=BC=1,再求出AD的长,然后根据等底等高的三角形的面积相等求出△ACD的面积,再根据三角板所扫过的面积=S扇形BCD+S扇形ACA1+S△ACD,然后列式计算即可得解;
(4)根据垂线段最短的性质,过点C作CE⊥AB于E,根据三角形的面积列式求出CE的长,再根据AB边扫过的面积等于三角板扫过的面积减去△BCE、△A1CE1、扇形ECE1的面积,列式进行计算即可得解.
(2)根据扇形的面积公式列式计算即可得解;
(3)设弧BB1与AB相交于D,可得△BCD是等边三角形,根据等边三角形的性质求出BD=BC=1,再求出AD的长,然后根据等底等高的三角形的面积相等求出△ACD的面积,再根据三角板所扫过的面积=S扇形BCD+S扇形ACA1+S△ACD,然后列式计算即可得解;
(4)根据垂线段最短的性质,过点C作CE⊥AB于E,根据三角形的面积列式求出CE的长,再根据AB边扫过的面积等于三角板扫过的面积减去△BCE、△A1CE1、扇形ECE1的面积,列式进行计算即可得解.
解答:解:(1)∵∠ACB=90°,AB=2,∠A=30°,
∴BC=
AB=
×2=1,
根据勾股定理,AC=
=
=
,
∴弧AA1=
=
π;
(2)扇形ACA1的面积=
=
π;
(3)设弧BB1与AB相交于D,
∵∠ACB=90°,∠A=30°,
∴∠B=90°-30°=60°,
又∵BC=CD,
∴△BCD是等边三角形,
∴BD=BC=1,
∴AD=AB-BD=2-1=1,
∴S△ACD=
S△ABC=
×
×1×
=
,
∴三角板所扫过的图形面积=S扇形BCD+S扇形ACA1+S△ACD,
=
+
+
,
=
π+
;
(4)过点C作CE⊥AB于E,
S△ABC=
AB•CE=
BC•AC,
即
×2×CE=
×1×
,
解得CE=
,
S△BCE+S△A1CE1=S△ABC=
×1×
=
,
S扇形ECE1=
=
π,
∴AB边所扫过的图形面积=(
π+
)-
-
π=
π-
.
∴BC=
| 1 |
| 2 |
| 1 |
| 2 |
根据勾股定理,AC=
| AB2-BC2 |
| 22-12 |
| 3 |
∴弧AA1=
90•π•
| ||
| 180 |
| ||
| 2 |
(2)扇形ACA1的面积=
90•π•
| ||
| 360 |
| 3 |
| 4 |
(3)设弧BB1与AB相交于D,
∵∠ACB=90°,∠A=30°,
∴∠B=90°-30°=60°,
又∵BC=CD,
∴△BCD是等边三角形,
∴BD=BC=1,
∴AD=AB-BD=2-1=1,
∴S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 4 |
∴三角板所扫过的图形面积=S扇形BCD+S扇形ACA1+S△ACD,
=
| 60•π•12 |
| 360 |
90•π•
| ||
| 360 |
| ||
| 4 |

=
| 11 |
| 12 |
| ||
| 4 |
(4)过点C作CE⊥AB于E,
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
即
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
解得CE=
| ||
| 2 |
S△BCE+S△A1CE1=S△ABC=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
S扇形ECE1=
90•π•(
| ||||
| 360 |
| 3 |
| 16 |
∴AB边所扫过的图形面积=(
| 11 |
| 12 |
| ||
| 4 |
| ||
| 2 |
| 3 |
| 16 |
| 35 |
| 48 |
| ||
| 4 |
点评:本题考查了旋转的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,勾股定理的应用,弧长的计算,扇形的面积公式,仔细分析图形确定出三角板本身以及边AC、AB所扫过的面积的组成是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
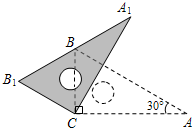 如图,三角板ABC中,∠ACB=90°,∠A=30°,AB=16cm,将三角板ABC绕直角顶点C逆时针旋转,当起始位置时的点B恰好落在边A1B1上时,BB1的长是
如图,三角板ABC中,∠ACB=90°,∠A=30°,AB=16cm,将三角板ABC绕直角顶点C逆时针旋转,当起始位置时的点B恰好落在边A1B1上时,BB1的长是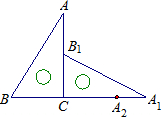 如图直角三角板ABC中,∠A=30°,BC=3cm,将直角三角板ABC绕着直角顶点C顺时针方向旋转90°至△A1B1C1的位置,再沿CB向左平移使点B1落在△ABC的斜边AB上,点A1平移到点A2的位置,则点A?A1?A2运动的路径长度是
如图直角三角板ABC中,∠A=30°,BC=3cm,将直角三角板ABC绕着直角顶点C顺时针方向旋转90°至△A1B1C1的位置,再沿CB向左平移使点B1落在△ABC的斜边AB上,点A1平移到点A2的位置,则点A?A1?A2运动的路径长度是 应点A′落在AB边的起始位置上时即停止转动,则点B转过的路径长为
应点A′落在AB边的起始位置上时即停止转动,则点B转过的路径长为 如图,三角板ABC中,∠ACB=90°,∠B=30°,BC=6.三角板绕直角顶点C逆时针旋转,当点A的对应点A'落在AB边的起始位置上时即停止转动,则点B转过的路径长为
如图,三角板ABC中,∠ACB=90°,∠B=30°,BC=6.三角板绕直角顶点C逆时针旋转,当点A的对应点A'落在AB边的起始位置上时即停止转动,则点B转过的路径长为 如图,三角板ABC中,∠ACB=90°,∠B=30°,BC=6.三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,则阴影部分的面积为
如图,三角板ABC中,∠ACB=90°,∠B=30°,BC=6.三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,则阴影部分的面积为