题目内容
6.某市计划修建50千米的地铁,开工后每月的进度比原计划提高了10%,结果提前2个月完成了任务,设原计划每月修建地铁x千米,由题意可列方程为( )| A. | $\frac{50}{x}$-$\frac{50}{x(1+10%)}$=2 | B. | $\frac{50}{x(1+10%)}$-$\frac{50}{x}$-=2 | C. | $\frac{50}{x}$-$\frac{50}{10%x}$=2 | D. | $\frac{50}{x(1+10%)}$+$\frac{50}{x}$-=2 |
分析 关键描述语为:“提前2个月完成了任务”;等量关系为:原计划用的月数-实际用的月数=提前月数.
解答 解:设原计划每月修建地铁x千米,则原计划用的月数为:$\frac{50}{x}$,实际用的月数为:$\frac{50}{x(1+10%)}$.
所列方程为:$\frac{50}{x}$-$\frac{50}{x(1+10%)}$=2.
故选A.
点评 本题考查了由实际问题抽象出分式方程,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
16.安徽省,政府工作报告》指出,2017年全年将实施亿元以上技改项目1000项,完成投资6600亿元,把6600亿用科学记数法可表示为( )
| A. | 6.6×103 | B. | 66×1010 | C. | 6.600×1011 | D. | 0.66×1012 |
1. 某中学在安全工作月中,进行了“防自然灾害-地震知识知多少”专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,花粉等级后的数据整理如下表:
某中学在安全工作月中,进行了“防自然灾害-地震知识知多少”专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,花粉等级后的数据整理如下表:
(1)表中m的值为0.6,n的值为36;
(2)根据表中的数据,请你计算“非常了解”的频率在如图中对应的扇形的圆心角的度数,并补全扇形统计图;
(3)若校一共有2400名学生,请根据调查结果估计全校学生中“比较了解”的人数为多少?
 某中学在安全工作月中,进行了“防自然灾害-地震知识知多少”专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,花粉等级后的数据整理如下表:
某中学在安全工作月中,进行了“防自然灾害-地震知识知多少”专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,花粉等级后的数据整理如下表:| 等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
| 频数 | 40 | 120 | n | 4 |
| 频率 | 0.2 | m | 0.18 | 0.02 |
(2)根据表中的数据,请你计算“非常了解”的频率在如图中对应的扇形的圆心角的度数,并补全扇形统计图;
(3)若校一共有2400名学生,请根据调查结果估计全校学生中“比较了解”的人数为多少?
11.下列运算中,正确的是( )
| A. | a6÷a2=a3 | B. | a3•a=a4 | C. | (-a2)3=a6 | D. | 2a3+a3=3a6 |
15. 如图是由5个相同的小正方体构成的几何体,其主视图是( )
如图是由5个相同的小正方体构成的几何体,其主视图是( )
 如图是由5个相同的小正方体构成的几何体,其主视图是( )
如图是由5个相同的小正方体构成的几何体,其主视图是( )| A. |  | B. |  | C. |  | D. |  |
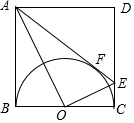 如图,在正方形ABCD中,以BC为直径的正方形内,作半圆O,AE切半圆于点F交CD于E.
如图,在正方形ABCD中,以BC为直径的正方形内,作半圆O,AE切半圆于点F交CD于E.