题目内容
20.已知∠AOB=30°,点P在△AOB内部,P1与P关于OB对称,P2与P关于OA对称,则∠P1OP2的度数是( )| A. | 90° | B. | 45° | C. | 30° | D. | 60° |
分析 画出图形,连接OP,根据对称轴是对称点连线的垂直平分线可知:OB是PP1的垂直平分线,OA是PP2的垂直平分线,由垂直平分线性质得:OP=OP1=OP2,所以根据等腰三角形三线合一得:∠P1OB=∠POB和∠P2OA=∠POA,则所求的∠P1OP2的度数是∠AOB的度数的2倍.
解答 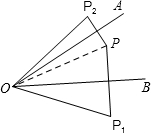 解:如图所示,连接OP,
解:如图所示,连接OP,
∵P1与P关于OB对称,
∴OB是PP1的垂直平分线,
∴OP=OP1,
∴∠P1OB=∠POB,
同理得:∠P2OA=∠POA,
∴∠POA+∠POB=∠P2OA+∠P1OB,
∴∠P2OP1=2∠AOB=2×30°=60°,
故选D.
点评 本题考查了轴对称的性质,熟练掌握如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.而垂直平分线上的点与线段两个端点的距离相等;得到等腰三角形后,要熟知等腰三角形的性质:①等边对等角,②三线合一等;使问题得对解决.

练习册系列答案
相关题目
10.一元二次方程ax2+bx+c=0有一个根为0,则必有( )
| A. | a=0 | B. | b=0 | C. | c=0 | D. | a+b+c=0 |
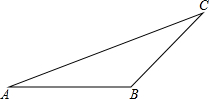 如图,已知△ABC,用直尺和圆规求作一直线AD,使直线过顶点A,且平分△ABC的面积(不需写作法,保留作图痕迹)
如图,已知△ABC,用直尺和圆规求作一直线AD,使直线过顶点A,且平分△ABC的面积(不需写作法,保留作图痕迹)