题目内容
 如图,在矩形ABCD中,AB=3,AD=4,P是AD上不与A、D重合的一动点,PE⊥AC,PF⊥BD,E、F为垂足,则PE+PF的值为
如图,在矩形ABCD中,AB=3,AD=4,P是AD上不与A、D重合的一动点,PE⊥AC,PF⊥BD,E、F为垂足,则PE+PF的值为考点:矩形的性质
专题:
分析:连接OP,过点A作AG⊥BD于G,利用勾股定理列式求出BD,再利用三角形的面积求出AG,然后根据△AOD的面积求出PE+PF=AG.
解答: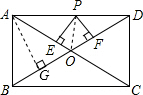 解:如图,连接OP,过点A作AG⊥BD于G,
解:如图,连接OP,过点A作AG⊥BD于G,
∵AB=3,AD=4,
∴BD=
=
=5,
S△ABD=
AB•AD=
BD•AG,
即
×3×4=
×5×AG,
解得AG=
,
在矩形ABCD中,OA=OD,
∵S△AOD=
OA•PE+
OD•PF=
OD•AG,
∴PE+PF=AG=
.
故PE+PF=
.
 解:如图,连接OP,过点A作AG⊥BD于G,
解:如图,连接OP,过点A作AG⊥BD于G,∵AB=3,AD=4,
∴BD=
| AB2+AD2 |
| 32+42 |
S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
即
| 1 |
| 2 |
| 1 |
| 2 |
解得AG=
| 12 |
| 5 |
在矩形ABCD中,OA=OD,
∵S△AOD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴PE+PF=AG=
| 12 |
| 5 |
故PE+PF=
| 12 |
| 5 |
点评:本题考查了矩形的性质,勾股定理,三角形的面积,熟练掌握各性质并利用三角形的面积列出方程是解题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
在正三角形、平行四边形、矩形和圆这四种图形中,既是轴对称图形又是中心对称图形的有( )种.
| A、1 | B、2 | C、3 | D、4 |
以下是代数式的是( )
| A、m=ab |
| B、(a+b)(a-b)=a2 |
| C、a+1-b2 |
| D、S=πR2 |
 已知二次函数y=ax2+bx+c的图象如图所示.下列结论:
已知二次函数y=ax2+bx+c的图象如图所示.下列结论: 如图,在平面直角坐标系中,点A和点B分别在x轴和y轴的正半轴上,OA=OB=a,以线段AB为边在第一象限作正方形ABCD,CD的延长线交x轴于点E,再以CE为边作第二个正方形ECGF,…,依此方法作下去,则第2014个正方形的边长是
如图,在平面直角坐标系中,点A和点B分别在x轴和y轴的正半轴上,OA=OB=a,以线段AB为边在第一象限作正方形ABCD,CD的延长线交x轴于点E,再以CE为边作第二个正方形ECGF,…,依此方法作下去,则第2014个正方形的边长是