题目内容

函数y=-x2+2x的图象是一条
 
，开口向
 
，对称轴是
 
，顶点坐标为
 
．
分析：根据抛物线图象性质解题．
解答：解：
∵a=-1＜0，
∴开口向下，对称轴x=-
b
2a
=1，顶点坐标为（-
b
2a
=1，
4ac-b2
4a
=1），即（1，1）．
∴函数y=-x2+2x的图象是一条抛物线，开口向下，对称轴是x=1，顶点坐标为（1，1）．
点评：主要考查了二次函数的性质和求抛物线的顶点坐标、对称轴的方法．
练习册系列答案
相关题目
10、若把二次函数y=x2-2x-3化为y=（x-h）2+k的形式，其中h，k为常数，则h+k=
-3
．
29、已知二次函数y=x2-2x-3的图象与x轴交于A、B两点（A在B的左侧），与y轴交于点C，顶点为D．
（1）求点A、B、C、D的坐标，并在下面直角坐标系中画出该二次函数的大致图象；
（2）说出抛物线y=x2-2x-3可由抛物线y=x2如何平移得到？
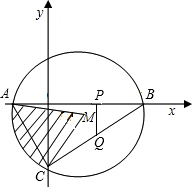精英家教网如图，已知二次函数y=x2-2x-3的图象与x轴交于点A、B两点，与y轴交于C点，⊙M是△ABC的外接圆．
（1）求阴影部分扇形AMC的面积；
（2）在x轴的正半轴上有一点P，作PQ⊥x轴交BC于Q，设PQ=K．
①设△OPQ的面积为S，求S关于K的函数关系式，并求出S的最大值；
②△CMQ能否与△AOC相似？若能，求出K的值；若不能，说明理由．
（2013•余姚市模拟）函数y=
k
x
和y=-
k
x
（k≠0）的图象关于y轴对称，我们把函数y=
k
x
和y=-
k
x
（k≠0）叫做互为“镜子”函数．类似地，如果函数y=f（x）和y=h（x）的图象关于y轴对称，那么我们就把函数y=f（x）和y=h（x）叫做互为“镜子”函数．
（1）请写出函数y=3x-4的“镜子”函数：
y=-3x-4
y=-3x-4
；
（2）函数
y=x2+2x+3
y=x2+2x+3
的“镜子”函数是y=x2-2x+3；
（3）如图，一条直线与一对“镜子”函数y=
2
x
（x＞0）和y=-
2
x
（x＜0）的图象分别交于点A、B、C，如果CB：AB=1：2，点C在函数y=-
2
x
（x＜0）的“镜子”函数上的对应点的横坐标是
1
2
，求点B的坐标．
定义符号yx表示与自变量x所对应的函数值．例如对于函数y=x2-2x+4，当x=2时，对应的函数值y=4，则可以写为：y2=4．在二次函数y=ax2+bx+c（a＞0）中，若yt+1=y-t+1对任意实数t都成立，那么下列结论错误的是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网